kategorier: Interessante fakta, Praktisk elektronik
Antal visninger: 231,928
Kommentarer til artiklen: 9
Kondensatorer: formål, enhed, driftsprincip
 I alle radio- og elektroniske enheder undtagen transistorer og mikrokredsløb anvendes kondensatorer. I nogle kredsløb er der flere af dem, i andre mindre, men absolut uden kondensatorer er der praktisk talt intet elektronisk kredsløb.
I alle radio- og elektroniske enheder undtagen transistorer og mikrokredsløb anvendes kondensatorer. I nogle kredsløb er der flere af dem, i andre mindre, men absolut uden kondensatorer er der praktisk talt intet elektronisk kredsløb.
I dette tilfælde kan kondensatorer udføre en række forskellige opgaver på enheder. Først og fremmest er dette containere i filtrene på ensretter og stabilisatorer. Ved hjælp af kondensatorer overføres et signal mellem forstærkertrinnene, lav- og højfrekvensfiltre bygges, tidsintervaller i tidsforsinkelser indstilles, og svingningsfrekvensen i forskellige generatorer vælges.
Kondensatorer fører fra leiden bankersom i midten af 1700-tallet blev brugt i deres eksperimenter af den hollandske videnskabsmand Peter van Mushenbrook. Han boede i byen Leiden, så det er let at gætte, hvorfor denne bank blev kaldt.
Faktisk var dette en almindelig glaskrukke, foret indvendigt og udvendigt med en tinfolie - staniol. Det blev brugt til de samme formål som moderne aluminium, men så var aluminium endnu ikke åbent.
Den eneste strømkilde i disse dage var en elektroforemaskine, der var i stand til at udvikle en spænding på op til flere hundrede kilovolt. Det var fra hende, de anklagede en Leyden-krukke. I fysikens lærebøger beskrives en sag, når Mushenbrook udledte sin dåse gennem en kæde med ti vagter, der holder hænderne.
På det tidspunkt vidste ingen, at konsekvenserne kunne være tragiske. Slaget viste sig at være ganske følsomt, men ikke dødeligt. Det kom ikke til dette, fordi kapaciteten i Leyden-krukken var ubetydelig, impulsen viste sig at være meget kortvarig, så afladningskraften var lille.
Hvordan er kondensatoren
Kondensatorens anordning er praktisk taget ikke forskellig fra Leiden-dåsen: alle de samme to plader, adskilt af et dielektrikum. Dette er, hvordan kondensatorer er afbildet på moderne elektriske kredsløb. Figur 1 viser en skematisk struktur af en flad kondensator og formlen til dens beregning.
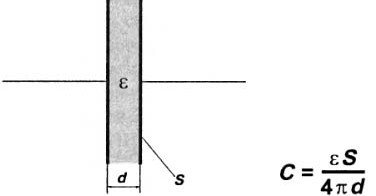
Figur 1. Flad kondensatorenhed
Her er S pladeområdet i kvadratmeter, d er afstanden mellem pladerne i meter, C er kapacitansen i farader, ε er mediets dielektriske konstant. Alle værdier inkluderet i formlen er angivet i SI-systemet. Denne formel er gyldig for den enkleste flade kondensator: du kan blot placere to metalplader ved siden af dem, hvorfra der drages konklusioner. Luft kan fungere som et dielektrikum.
Fra denne formel kan det forstås, at kondensatoren er større, jo større er arealet af pladerne, og desto mindre er afstanden mellem dem. For kondensatorer med en anden geometri kan formlen være forskellig, for eksempel til kapacitansen af en enkelt leder eller elektrisk kabel. Men afhængigheden af kapacitansen af pladenes område og afstanden imellem dem er den samme som for en flad kondensator: jo større areal og mindre afstand, desto større er kapacitansen.
Faktisk er pladerne ikke altid flade. For mange kondensatorer, for eksempel papir, er pladerne aluminiumsfolie rullet sammen med et papir dielektrikum i en tæt kugle i form af et metalhus.
For at øge den elektriske styrke imprægneres tyndt kondensatorpapir med isolerende sammensætninger, oftest transformerolie. Dette design giver dig mulighed for at fremstille kondensatorer med en kapacitet på op til flere hundrede mikrofarader. Kondensatorer med anden dielektrik er på lignende måde arrangeret.
Formlen indeholder ingen begrænsninger for pladen S's område og afstanden mellem pladerne d.Hvis vi antager, at pladerne kan tages meget langt og på samme tid gør pladenes område meget lille, forbliver en vis kapacitet, omend lille, stadig. Denne begrundelse antyder, at selv kun to ledere, der er placeret i nabolaget, har en elektrisk kapacitet.
Denne omstændighed er vidt brugt i højfrekvente teknologi: i nogle tilfælde fremstilles kondensatorer simpelthen i form af trykte kredsløb, eller endda bare to ledninger, der er snoet sammen i polyethylenisolering. Almindelige trådnudler eller -kabler har også en kapacitet, og med stigende længde stiger det.
Foruden kapacitet C har ethvert kabel også modstand R. Begge disse fysiske egenskaber er fordelt langs kablets længde, og når de sender pulserede signaler, fungerer de som en integrerende RC-kæde, vist i figur 2.

Figur 2
I figuren er alt simpelt: her er kredsløbet, her er indgangssignalet, men her er det ved udgangen. Impulsen er forvrænget til genkendelse, men dette gøres med vilje, som kredsløbet er samlet til. I mellemtiden taler vi om effekten af kabelkapacitansen på pulssignalet. I stedet for en impuls, vil en sådan "klokke" vises på den anden ende af kablet, og hvis impulsen er kort, er den muligvis slet ikke den anden ende af kablet, den er helt væk.
Historisk kendsgerning
Her er det helt passende at huske historien om, hvordan det transatlantiske kabel blev lagt. Det første forsøg i 1857 mislykkedes: telegrafpunkterne - bindestreger (rektangulære pulser) blev forvrænget, så intet kunne adskilles i den anden ende af 4000 km-linjen.
Et andet forsøg blev gjort i 1865. På dette tidspunkt havde den engelske fysiker W. Thompson udviklet en teori om dataoverførsel over lange linjer. I lyset af denne teori viste kabelføringen sig at være mere vellykket, og vi var i stand til at modtage signaler.
For denne videnskabelige brik tildelte dronning Victoria videnskabsmanden ridderlandskab og titlen Lord Kelvin. Det var navnet på den lille by ved Irlands kyst, hvor kabelføringen begyndte. Men dette er bare et ord, og nu vender vi tilbage til det sidste bogstav i formlen, nemlig til dielektrisk konstant for mediet ε.
Lidt om dielektrik
Dette ε er i nævneren af formlen, derfor vil dens stigning medføre en stigning i kapacitet. For de fleste anvendte dielektriske stoffer, såsom luft, lavsan, polyethylen, fluoroplast, er denne konstant næsten den samme som for vakuum. Men på samme tid er der mange stoffer, hvis dielektriske konstant er meget højere. Hvis luftkondensatoren er fyldt med acetone eller alkohol, øges dens kapacitet hver 15. ... 20.
Men sådanne stoffer udover høj ε har også en tilstrækkelig høj ledningsevne, derfor vil en sådan kondensator ikke holde en ladning godt, den vil hurtigt udledes gennem sig selv. Dette skadelige fænomen kaldes lækstrøm. Derfor udvikles specielle materialer til dielektrik, der med en høj specifik kapacitans af kondensatorer tilvejebringer acceptable lækstrømme. Dette forklarer mangfoldigheden af typer og typer kondensatorer, som hver især er designet til specifikke forhold.
Elektrolytisk kondensator
Den højeste specifikke kapacitet (kapacitet / volumen-forhold) elektrolytiske kondensatorer. Kapaciteten af "elektrolytter" når op til 100.000 mikrofarader, og driftsspændingen er op til 600V. Sådanne kondensatorer fungerer kun godt ved lave frekvenser, oftest i filtre med strømforsyning. Elektrolytiske kondensatorer tændes i polaritet.
Elektroderne i sådanne kondensatorer er en tynd film af metaloxid, så ofte kaldes disse kondensatorer oxid. Et tyndt luftlag mellem sådanne elektroder er ikke en særlig pålidelig isolator, derfor indføres et elektrolytlag mellem oxidpladerne. Oftest er dette koncentrerede opløsninger af syrer eller alkalier.
Figur 3 viser en af disse kondensatorer.

Figur 3. Elektrolytisk kondensator
For at evaluere kondensatorens størrelse blev der fotograferet en simpel matchbox ved siden af. Ud over en tilstrækkelig stor kapacitet i figuren kan du også se den procentuelle tolerance: ikke mindre end 70% af den nominelle.
I de dage, hvor computere var store og kaldte computere, var sådanne kondensatorer i drev (i den moderne HDD). Sådanne drevs informationskapacitet kan nu kun give et smil: 5 megabyte information blev lagret på to diske med en diameter på 350 mm, og selve enheden vejer 54 kg.
Hovedformålet med superkapsler, der er vist på figuren, var tilbagetrækning af magnetiske hoveder fra arbejdsområdet på disken under et pludseligt strømafbrydelse. Sådanne kondensatorer kunne opbevare en ladning i flere år, som blev testet i praksis.
Lidt lavere med elektrolytiske kondensatorer vil blive tilbudt at udføre nogle enkle eksperimenter for at forstå, hvad en kondensator kan gøre.
At arbejde i vekslingskredsløb produceres ikke-polære elektrolytiske kondensatorer, det er bare svært at få dem af en eller anden grund. For på en eller anden måde at omgå dette problem inkluderer almindelige polære "elektrolytter" mod-sekventiel: plus-minus-minus-plus.
Hvis den polære elektrolytiske kondensator er inkluderet i vekselstrømskredsløbet, opvarmes den først, og derefter høres en eksplosion. Indenlandske gamle kondensatorer spredt i alle retninger, mens importerede har en speciel enhed, der undgår høje skud. Dette er normalt enten et tværsnit på bunden af kondensatoren eller et hul med en gummiprop placeret på samme sted.
De kan ikke lide elektrolytiske kondensatorer med høj spænding, selvom polariteten overholdes. Derfor bør du aldrig anbringe "elektrolytter" i et kredsløb, hvor der forventes en spænding tæt på det maksimale for en given kondensator.
Nogle gange stiller begyndere i nogle, også velrenommerede fora, spørgsmålet: "Kondensatoren 470µF * 16V er angivet på diagrammet, og jeg har 470µF * 50V, kan jeg sige det?" Ja, det kan du selvfølgelig, men den omvendte udskiftning er uacceptabel.
Kondensator kan lagre energi
For at håndtere denne erklæring hjælper et simpelt diagram vist i figur 4.
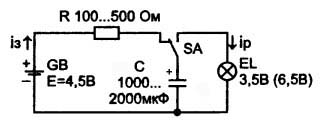
Figur 4. Kredsløb med kondensator
Hovedpersonen i dette kredsløb er en elektrolytisk kondensator C med tilstrækkelig stor kapacitet til at ladning-afladningsprocesserne fortsætter langsomt og endda meget tydeligt. Dette gør det muligt at observere driften af kredsløbet visuelt ved hjælp af et konventionelt lys fra en lommelygte. Disse lys har længe givet vej til moderne LED'er, men pærer til dem sælges stadig. Derfor er det meget let at samle et kredsløb og udføre enkle eksperimenter.
Måske vil nogen sige: ”Hvorfor? Når alt kommer til alt er alt indlysende, og selvom du læser beskrivelsen ... ” Der synes ikke at være noget at argumentere her, men noget, også den enkleste, forbliver i hovedet i lang tid, hvis dens forståelse kom gennem hænder.
Så kredsløbet er samlet. Hvordan fungerer hun?
I kontakten SA, som er vist i diagrammet, lades kondensatoren C fra strømkilden GB gennem modstanden R i kredsløbet: + GB __ R __ SA __ C __-GB. Opladningsstrømmen i diagrammet vises med en pil med indekset iз. Processen med at oplade en kondensator er vist i figur 5.
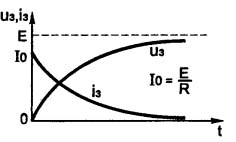
Figur 5. Kondensatoropladningsproces
Figuren viser, at spændingen på kondensatoren stiger langs en kurvelinie, i matematik kaldet eksponenten. Ladestrømmen afspejler direkte ladespændingen. Når spændingen over kondensatoren stiger, bliver ladestrømmen mindre og mindre. Og kun i det første øjeblik svarer til formlen vist i figuren.
Efter et stykke tid lades kondensatoren fra 0V til spændingen i strømkilden, i vores kredsløb til 4,5V. Hele spørgsmålet er, hvordan er dette tidspunkt at bestemme, hvor længe man skal vente, hvornår oplader kondensatoren?
Tau tidskonstant τ = R * C
I denne formel multipliseres simpelthen modstanden og kapacitansen af en seriekoblet modstand og kondensator.Hvis uden at forsømme SI-systemet, erstatte modstanden i Ohms, kapacitansen i Farads, vil resultatet være i sekunder. Det er denne gang, der er nødvendigt for kondensatoren at oplade op til 36,8% af spændingen i strømkilden. Derfor kræves der en tid på 5 * t for et gebyr på næsten 100%.
Når man forsømmer SI-systemet, erstattes modstanden i Ohms ofte med formlen, og kapacitansen er i mikrofarader, så vil tiden vise sig i mikrosekunder. I vores tilfælde er det mere praktisk at få resultatet i sekunder, som du bare skal multiplicere mikrosekunderne med en million, eller mere enkelt sagt, flytte de komma seks tegn til venstre.
For kredsløbet vist i figur 4 med en kondensator på 2000 μF og en modstandsmodstand på 500 Ω vil tidskonstanten være τ = R * C = 500 * 2000 = 1.000.000 mikrosekunder eller nøjagtigt et sekund. Således bliver du nødt til at vente i cirka 5 sekunder, indtil kondensatoren er fuldt opladet.
Hvis afbryderen SA, efter den specificerede tid er gået, drejes til den rigtige position, udledes kondensatoren C gennem EL-pæren. I dette øjeblik vil der opstå en kort blitz, kondensatoren udlades, og lyset slukker. Kondensatorens udladningsretning vises med en pil med indekset ip. Udladningstiden bestemmes også af tidskonstanten τ. Udladningsgrafen er vist i figur 6.
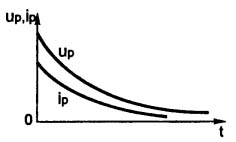
Figur 6. Kondensatorudladningsgraf
Kondensator passerer ikke jævnstrøm
For at verificere denne erklæring vil et endnu enklere skema, vist i figur 7, hjælpe.
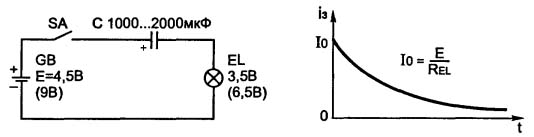
Figur 7. Kredsløb med en kondensator i et jævnstrømskredsløb
Hvis du lukker kontakten SA, følger en kort blink af pæren, der indikerer, at kondensatoren C lades gennem pæren. Ladegrafen vises også her: på det øjeblik, omskifteren lukker, er strømmen maksimal, når kondensatoren oplades, aftager den, og efter et stykke tid stopper den helt.
Hvis kondensatoren er af god kvalitet, dvs. med en lille lækstrøm (selvudladning) vil den gentagne lukning af kontakten ikke føre til blitz. For at få en anden flash, skal kondensatoren aflades.
Kondensator i strømfiltre
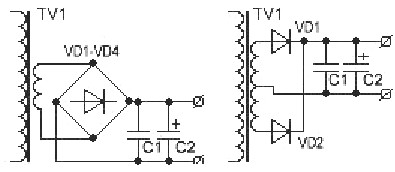
Kondensatoren placeres normalt efter ensretteren. Oftest fremstilles ensretter halvbølge. De mest almindelige ensretterkredsløb er vist i figur 8.
Figur 8. Likretterkredsløb
Halvbølge ensretter bruges som regel også ofte, i tilfælde hvor belastningen er ubetydelig. Den mest værdifulde kvalitet af sådanne ensretter er enkelhed: kun en diode og transformervikling.
For en halvbølge ensretter kan filterkondensatorens kapacitet beregnes med formlen
C = 1.000.000 * Po / 2 * U * f * dU, hvor C er kondensatoren μF, Po er belastningseffekten W, U er spændingen ved ensretterens udgang V, f er frekvensen for vekselstrømspændingen Hz, dU er krusningsamplituden V
Et stort antal i tælleren på 1.000.000 konverterer kapacitansen for kondensatoren fra system Farads til mikrofarader. De to i nævneren repræsenterer antallet af halvperioder af ensretteren: for en halvbølge på sin plads vises en enhed
C = 1.000.000 * Po / U * f * dU,
og for en trefaset ensretter, vil formlen have formen C = 1.000.000 * Po / 3 * U * f * dU.
Superkapacitor - Ionistor
For nylig blev en ny klasse af elektrolytiske kondensatorer, den såkaldte ionistor. I sine egenskaber ligner det dog et batteri, dog med flere begrænsninger.
Ionistoren oplades til den nominelle spænding på kort tid, bogstaveligt talt på få minutter, så det tilrådes at bruge det som en backup-strømkilde. Faktisk er ionistoren en ikke-polær enhed, det eneste, der bestemmer dens polaritet, er opladning fra fabrikken. For ikke at forveksle denne polaritet i fremtiden, vises den med + -tegnet.
En vigtig rolle spilles af ionistorenes driftsbetingelser. Ved en temperatur på 70 ° C ved en spænding på 0,8 af den nominelle garanterede holdbarhed på højst 500 timer.Hvis enheden fungerer med en spænding på 0,6 fra den nominelle, og temperaturen ikke overstiger 40 grader, er korrekt drift mulig i 40.000 timer eller mere.
De mest almindelige ionistor-applikationer er backup-strømkilder. Dette er hovedsageligt hukommelseschips eller elektroniske ure. I dette tilfælde er ionistorens hovedparameter en lav lækstrøm, dets selvudladning.
Helt lovende er brugen af ionistorer i forbindelse med solcellepaneler. Det påvirker også ikke-kritik af ladningens tilstand og et næsten ubegrænset antal ladeafladningscyklusser. En anden værdifuld egenskab er, at ionistoren er vedligeholdelsesfri.
Indtil videre har det vist sig at fortælle, hvordan og hvor elektrolytiske kondensatorer fungerer, og hovedsageligt i jævnstrømskredsløb. Betjeningen af kondensatorer i vekslingskredsløb vil blive beskrevet i en anden artikel - Kondensatorer til AC elektriske installationer.
Boris Aladyshkin
P. S. En interessant brugssag til kondensatorer: kondensator svejsning
Se også på elektrohomepro.com
: