"Alt flyder", eller Ohms lov for de nysgerrige

Selv den sidste loafer, der har studeret i nogen tid i 10. klasse, vil fortælle læreren det Ohms lov - dette er "U er lig med jeg gange R". Desværre vil den smarteste fremragende studerende sige lidt mere - den fysiske side af Ohms lov vil forblive et mysterium for ham i syv sæler. Jeg tillader mig at dele med mine kolleger min erfaring med at præsentere dette tilsyneladende primitive emne.

Formålet med min pædagogiske aktivitet var kunsten og den humanitære 10. klasse, hvis vigtigste interesser, som læseren gætter, lå meget langt fra fysik. Derfor blev undervisningen i dette emne overdraget forfatteren af ​​disse linjer, der generelt set underviser i biologi. Det var for et par år siden.

Lektionen om Ohms lov begynder med den trivielle erklæring om, at elektrisk strøm er bevægelsen af ​​ladede partikler i et elektrisk felt. Hvis kun en elektrisk kraft virker på en ladet partikel, accelererer partiklen i overensstemmelse med Newtons anden lov. Og hvis vektoren af ​​elektrisk kraft, der virker på den ladede partikel, er konstant på hele banen, er den lige så hurtig. Ligesom en vægt falder under tyngdekraften.

Men her falder faldskærm helt forkert. Hvis vi forsømmer vinden, er dens faldhastighed konstant. Selv en studerende i kunst- og humanitærklassen vil svare, at ud over tyngdekraften agerer endnu en styrke på den faldende faldskærm - luftmotstandens styrke. Denne kraft er i absolut værdi lig med styrken til tiltrækning af faldskærmen ved Jorden og er modsat den i retning. Hvorfor? Dette er lektiens centrale spørgsmål. Efter en vis diskussion konkluderer vi, at trækkraften stiger med stigende faldhastighed. Derfor accelererer det faldende legeme til en hastighed, hvor tyngdekraften og luftmodstanden udjævnes, og kroppen falder yderligere med en konstant hastighed.

Rigtigt, i tilfælde af en faldskærm, er situationen noget mere kompliceret. Faldskærmen åbnes ikke med det samme, og faldskærmsudøver accelererer til en markant højere hastighed. Og når faldskærmen allerede er åbnet, begynder faldet med en deceleration, der fortsætter, indtil tyngdekraften og luftmotstandskraften er afbalanceret.

For en faldskærmsladning med en total masse, der falder ned med konstant hastighed v, kan vi skrive: mg - F (v) = 0, hvor F (v) Er luftmodstanden betragtet som en funktion af faldhastigheden. Med hensyn til formen af ​​funktionen F (v) vi kan kun sige en ting indtil videre: det vokser monotont. Denne situation giver stabilisering af hastigheden.

I det enkleste tilfælde, når F (v) = k, den konstante hastighed, som faldskærmen falder med, er lig med mg / k. Lad os gøre noget konvertering nu. Lad faldskærmen falde fra en højde h. Derefter vil forskellen i kroppens potentielle energier før og efter faldet være lig mgh = mU, hvor U er den potentielle energi i kroppen af ​​enhedsmasse i en højde h, eller den potentielle forskel i gravitationsfeltet ved det indledende og sidste incidenspunkt.

I betragtning af det foregående opnår vi formlen: F (v) = mU / h. (1)

Og nu tilbage til lederen, gennem hvilken den elektriske strøm strømmer. Et stort antal ladede partikler bevæger sig langs lederen, der oftere kolliderer med atomer, jo hurtigere de flyver. Analogien med nedstigningen af ​​en faldskærm er ganske gennemsigtig, den eneste forskel er, at der er mange "faldskærme", og de bevæger sig ikke i tyngdepunktet, men i det elektriske felt. Under disse omstændigheder kan (1) omskrives i formen: F (v) = eU / l, (2)

hvor e er partikelladningen, er U den elektriske potentialeforskel ved enderne af lederen, l er længden af ​​lederen.Strømstyrken er åbenlyst lig med I = neS, hvor n er antallet af ladede partikler pr. Enhedsvolumen, S er tværsnitsarealet for lederen, er partikelhastigheden (for enkelthed antager vi, at alle ladede partikler er ens).

For at opnå afhængighed I (U) skal du udtrykkeligt kende afhængigheden F (). Den enkleste mulighed (F = k) giver øjeblikkeligt Ohms lov (I ~ U):

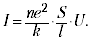
Værdien kaldes ledningsevne, og den gensidighed deraf kaldes modstand. Til ære for lovens opdager udtrykkes modstand normalt i ohm.

Værdien (ne2 / k) kaldes den specifikke ledningsevne, og dens inverse værdi kaldes den specifikke modstand. Disse værdier karakteriserer det materiale, som lederen består af. Det er signifikant, at konduktiviteten er proportional med antallet af ladede partikler pr. Enhedsvolumen (n). I metaller og elektrolytopløsninger er dette antal stort, men i dielektrik er det lille. Antallet af ladede partikler pr. Enhedsvolumen af ​​en gas kan afhænge af det påførte felt (dvs. det er en funktion af U), derfor gælder Ohm-loven ikke for gasser.

Da vi udledte Ohms lov, tog vi en ikke-indlysende antagelse. Vi accepterede, at den kraft, der hæmmer bevægelsen af ​​en ladet partikel, er proportional med dens hastighed. Naturligvis kunne man forsøge at retfærdiggøre denne idé på en eller anden måde, men den eksperimentelle verifikation ser meget mere overbevisende ud.

En eksperimentel verifikation af denne antagelse er selvfølgelig en verifikation af Ohms lov i sig selv, dvs. proportionaliteten af ​​U og I. Det ser ud til, at dette ikke er svært at gøre: vi har et voltmeter og et ammeter! Desværre er alt ikke så enkelt. Vi må forklare vores studerende, at et voltmeter, ligesom et ammeter, ikke måler spænding, men strømstyrken. Og vi har ret til at indstille volt på voltmeter-skalaen kun fordi vi oprindeligt kender Ohms lov, som vi ønsker at kontrollere. Brug for andre tilgange.

Du kan f.eks. Bruge følgende idé. Vi tilslutter n batterier i serie og antager, at spændingen i dette tilfælde steg n gange. Hvis Ohms lov er sandt, øges den aktuelle styrke også n gange, på grund af hvilken forholdet n / I (n) ikke afhænger af n. Denne antagelse er berettiget af erfaringer. Det er sandt, at batterierne også har intern modstand, og det er grunden til, at værdien af ​​n / I (n) vokser langsomt med stigende n, men det er ikke svært at rette op på dette. (G. Ohm selv målte stress på en anden måde, som eleverne kan læse om i lærebogen til G.Ya. Myakishev og andre.)

Vi stiller spørgsmålet: "" I den fjerne konstellation af Tau Ceti ", ikke Ohms lov, men loven fra den store lokale forsker Academic X. I henhold til X's lov er strømstyrken proportional med kvadratet af den potentielle forskel i endene af lederen. Hvordan afhænger partiklernes bremsekraft af deres hastighed på Tau Ceti? ” Ved hjælp af enkle transformationer konkluderer de studerende, at kraften er proportional med kvadratroten af ​​hastighed.

Og lad os nu gå videre til en anden proces: bevægelse af vand i et rør, i hvilke enderne skabes forskellige tryk. Her har vi en helt anden situation: ikke individuelle bevægelige partikler gnider mod et stationært materiale fordelt over hele volumen af ​​lederen, men lag af bevægelige partikler gnider mod hinanden. Og denne omstændighed ændrer grundlæggende al fysisk ræsonnement.

To kræfter virker på et separat lag vand, der bevæger sig i et rør:

a) forskellen i trykstyrker i enderne af laget;

b) friktionskraften mod de nærliggende vandlag.

Hvis der konstateres en konstant hastighed af laget, er disse kræfter lige og rettet i modsatte retninger.

Friktionskraften mod tilstødende lag af vand kan bremse bevægelsen, hvis og kun hvis forskellige lag af vand bevæger sig i forskellige hastigheder. I en leder afhænger hastigheden af ​​ladede partikler ikke af, om de befinder sig i kanten af ​​lederen eller i dets centrum, men vandet i midten af ​​røret bevæger sig hurtigt og langsomt langs kanterne på rørets overflade, vandhastigheden er nul.

En analog af den aktuelle styrke kan betragtes som vandstrøm, dvs. mængden af ​​vand, der strømmer ud af røret pr. tidsenhed. Da vandets hastighed i forskellige lag ikke er den samme, er beregningen af ​​strømningshastigheden ikke så enkel.En analog forskel i elektriske potentialer er trykforskellen i endene af røret.

Ligesom i en leder med strøm, observeres en direkte proportionalitet i røret med vand mellem trykforskellen ved enderne og strømningshastigheden. Men proportionalitetskoefficienten er helt anderledes. For det første afhænger vandstrømningshastigheden ikke kun af rørets tværsnitsareal, men også af dens form. Hvis røret er cylindrisk, er strømningshastigheden direkte proportional ikke med tværsnitsarealet, men med dets kvadrat (dvs. radius til fjerde grad). Denne afhængighed kaldes Poiseuille-loven.

Her er tiden til at huske forløbet anatomi, fysiologi og hygiejne, studeret i 9. klasse. Den menneskelige krop har et stort antal fartøjer, der er forbundet parallelt. Antag, at et af disse fartøjer er udvidet, og dets radius er lidt, kun fordoblet, steget. Hvor mange gange, med det samme tryk i enderne af karet, vil mængden af ​​blod, der passerer gennem det, stige? Tværsnitsarealet er proportionalt med radiusens kvadrat, og kvadratet af tværsnitsarealet er proportionalt med fjerde graders radius. Derfor, når radius er fordoblet, øges blodstrømmen 16 (!) Gange. Sådan er Poiseuille-lovens magt, der gør det muligt at skabe en meget effektiv mekanisme til omfordeling af blod mellem organer. Hvis elektroner ikke strømte gennem blodkar, ville deres strøm kun øges fire gange.

Beskrivelsen af ​​emnet beskrevet ovenfor er forskellig fra det traditionelle. For det første bruges tre lektioner til emnet, som med den aktuelle mangel på timer kan betragtes som en afviselig luksus for naturvidenskaberne. Dette er dog berettiget af det faktum, at det er muligt ganske enkelt og populært at afsløre den fysiske betydning af loven og udstyre studerende med en metode, som de kan bruge til at analysere en række fysiske processer: faldet af et legeme i luft, bevægelsen af ​​en væske i et rør, bevægelsen af ​​ladede partikler langs en leder og senere ved analyse af passage af elektrisk strøm gennem vakuum og gennem gasser.

Denne tilgang kaldes tværfaglig integration. Med sin hjælp demonstrerede vi for studerende fælles træk i fjerne fysiske sektioner i fjerne øjeblikke, vi viste, at fysik ikke er en "flok" af "fysiske love", der ikke er forbundet med hinanden, men en slank bygning. Det samme gælder naturligvis for andre videnskabelige discipliner. Og det ser ud til, at et irrationelt spild af træningstimer fuldt ud betaler sig.

Læs også:Sådan bruges et multimeter