Hvad er forbindelsen mellem trådafsnittene og kaninbestanden?

I 1202 udgav den italienske matematiker Leonardo Fibonacci sit arbejde under titlen "Book of Abacus" ("Book of Calculations"), hvor han også beskrev nummerserier udødeliggjort med hans navn. I et af kapitlerne prøver Fibonacci matematisk at vise, hvordan antallet af kaniner vil stige. Han betragtede følgende hypoteser som betingelser:

1) de første to måneder giver et par kaniner ikke afkom;

2) Fra den tredje måned giver et par kaniner et andet par kaniner.

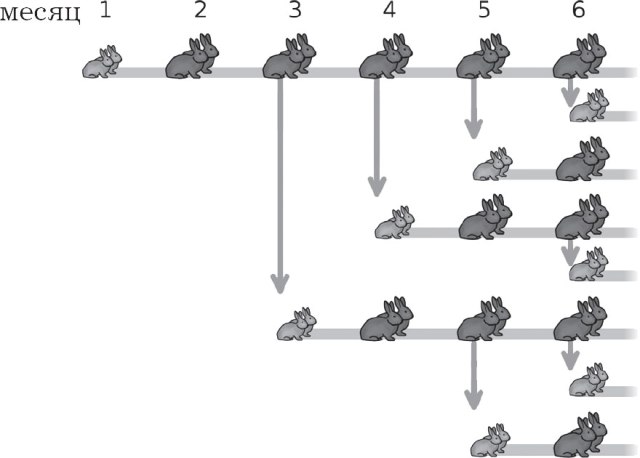
Som et resultat af at konstruere et vækstmønster for kaninbestanden opnår vi følgende række af numre, idet vi bemærker stigningen i antallet af kaniner hver måned:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

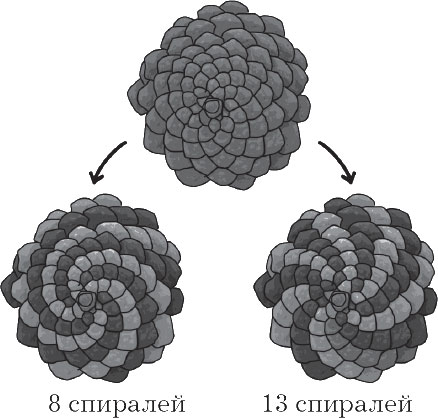
Hvis du omhyggeligt kigger på ujævnheden, vil du se, at dens overflade består af vægte, der er snoet i en spiral i overensstemmelse med Fibonacci-sekvensen. Mens de er i ananas eller i en solsikkeblomst, er de synlige med det blotte øje.

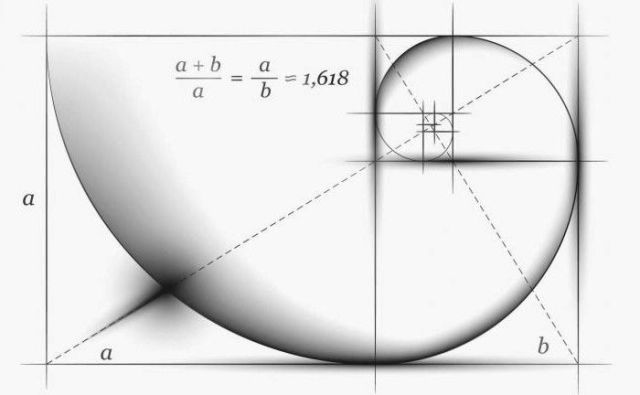
Siden tidspunktet for antikken med den gyldne forhold er antallet = 1.618. De gamle grækere overvejede værdien af ​​en ideel andel. Det gyldne forhold er forholdet mellem hvert efterfølgende tal i Fibonacci-serien og det foregående:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

De gamle grækere brugte det i arkitektur. Fasaden på Parthenon i Athen har meget ens proportioner med et rektangel bygget på princippet om det gyldne forhold.

Så hvad er skønheden ved rækkefølgen af ​​ledningstværsnit, nominelle strømme af elektriske og afskærmningsstrømme hos strømafbrydere? Byg en række numre med følgende værdier: 1,5; 2,5; 4; 6; 10; 16; 25; 40; 63...

Nominelle strømme af elektromagnetiske startere:

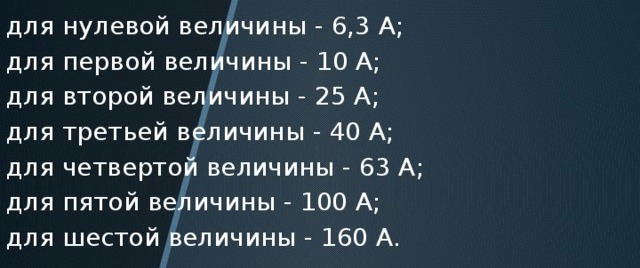
Så hvis du deler 2,5 / 1,5; 4 / 2,5; 6,3 / 4; 10 / 6,3; 16/10; 25/16; 40/25; 63/40så får vi cirka 1,6. Hvilket svarer til gylden ratio. Og afspejler naturens skønhed og geni, selv i vores kedelige ingeniørsystemer.

Hvad synes du? Er dette en ulykke?

Baseret på bogen "En stor roman om matematik. Verdenshistorie gennem matematikens prisme" af Michael Lone. Tak for anbefalingen fra Vladimir Kisel.

Alexey Bushnyaga