kategorier: Udvalgte artikler » Praktisk elektronik
Antal visninger: 124786
Kommentarer til artiklen: 1
Udførelse af en oscilloskopmåling
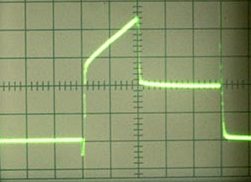Et digitalt oscilloskop er selvfølgelig meget mere avanceret end et konventionelt elektronisk, det giver dig mulighed for at huske bølgeformer, kan oprette forbindelse til en personlig computer, har matematisk behandling af resultater, skærmmarkører og meget mere. Men med alle fordelene har disse nye generation enheder en betydelig ulempe - dette er en høj pris.
Det er hun, der gør det digitale oscilloskop utilgængeligt til amatørformål, skønt der er ”lomme” -oscilloskoper, der kun er værd et par tusinde rubler, der sælges på Aliexpress, men det er ikke særlig praktisk at bruge dem. Bare et interessant legetøj. Derfor, mens vi vil tale om målinger ved hjælp af et elektronisk oscilloskop.
Om emnet at vælge et oscilloskop til brug i et hjemmelaboratorium på Internettet, kan du finde et tilstrækkeligt antal fora. Uden at benægte fordelene ved digitale oscilloskoper anbefales det i mange fora at vælge enkle, kompakte, pålidelige indenlandske oscilloskoper C1-73 og C1-101 og lignende, som vi mødte i denne artikel.
Til en rimelig pris giver disse enheder dig mulighed for at udføre de fleste amatørradioopgaver. Lad os i mellemtiden blive bekendt med de generelle principper for målinger ved hjælp af et oscilloskop.
Figur 1. Oscilloskop S1-73
Hvad et oscilloskop måler
Det målte signal føres til indgangen til den lodrette afbøjningskanal Y, som har en stor indgangsimpedans, sædvanligvis 1MΩ, og en lille indgangskapacitans, ikke mere end 40 pF, hvilket tillader introduktion af minimal forvrængning i det målte signal. Disse parametre er ofte indikeret ved siden af indgangen til den lodrette afbøjningskanal.
Figur 2. Oscilloskop C1-101
Høj indgangsimpedans er typisk for voltmetre, så det er sikkert at sige, at oscilloskopet måler spænding. Brug af eksterne indgangsdelere giver dig mulighed for at reducere inputkapacitansen og øge input impedansen. Det reducerer også påvirkningen af oscilloskopet på det undersøgte signal.
Det skal huskes, at der er specielle højfrekvente oscilloskoper, hvis indgangsimpedans kun er 50 ohm. I amatørradio praksis finder sådanne enheder ikke anvendelse. Derfor vil vi yderligere fokusere på konventionelle universelle oscilloskoper.
Kanal Y båndbredde
Oscilloskopet måler spændinger i et meget bredt område: fra jævnspændinger til spændinger med en tilstrækkelig høj frekvens. Spændingssvingningen kan være ganske forskellig fra titusinder af millivolt til titalls volt, og når der bruges eksterne skilleapparater op til flere hundrede volt.
Det skal huskes, at båndbredden for kanalen for den lodrette afvigelse Y db ikke mindre end 5 gange højere end frekvensen for det signal, der skal måles. Det vil sige, at forstærkeren af den lodrette afvigelse skal passere mindst den femte harmoni af det undersøgte signal. Dette er især påkrævet, når man studerer rektangulære pulser, der indeholder mange harmonikker, som vist i figur 3. Kun i dette tilfælde opnås et billede med minimal forvrængning på skærmen.
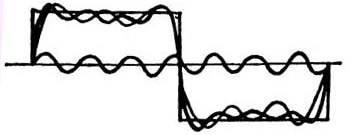
Figur 3. Syntese af et rektangulært signal fra harmoniske komponenter
Ud over den grundlæggende frekvens viser figur 3 den tredje og syvende harmonik. Når det harmoniske antal stiger, øges dets frekvens: hyppigheden af den tredje harmoniske er tre gange højere end den grundlæggende, den femte harmoniske er fem gange, den syvende er syv osv. Følgelig formindskes amplituden af de højere harmoniske: jo højere det harmoniske antal er, jo lavere er amplituden. Kun hvis forstærkeren af den lodrette kanal uden meget dæmpning kan gå glip af de højere harmoniske, vil billedet af pulsen være rektangulær.
Figur 4 viser bølgeformen af en krumning med utilstrækkelig kanal Y-båndbredde.
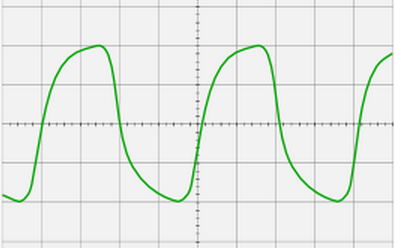
Figur 4
Slyngen med en frekvens på 500 KHz ser sådan ud på skærmen på et OMSh-3M oscilloskop med en båndbredde på 0 ... 25 KHz. Som om rektangulære pulser blev ført gennem et integrerende RC-kredsløb. Et sådant oscilloskop blev produceret af den sovjetiske industri til laboratoriearbejde i fysikundervisning i skoler. Selv denne enheds forsyningsspænding var af sikkerhedsmæssige årsager ikke 220, men kun 42V. Det er helt åbenlyst, at et oscilloskop med en sådan båndbredde gør det muligt at observere et signal med frekvenser på højst 5 kHz uden næsten ingen forvrængning.
For et konventionelt universelt oscilloskop er båndbredden oftest 5 MHz. Selv med et sådant bånd kan du se et signal op til 10 MHz og højere, men det modtagne billede på skærmen giver dig mulighed for kun at bedømme tilstedeværelsen eller fraværet af dette signal. Det vil være vanskeligt at sige noget om dens form, men i nogle situationer er formen ikke så vigtig: for eksempel er der en sinusformet generator, og det er nok til at sikre sig, at der er denne sinusform eller ikke. Bare en sådan situation er vist i figur 4.
Moderne computersystemer og kommunikationslinjer fungerer ved meget høje frekvenser i størrelsesordenen hundreder af megahertz. For at se sådanne høyfrekvente signaler skal oscilloskopets båndbredde være mindst 500 MHz. Et så bredt bånd "udvider" virkelig prisen på oscilloskopet.
Et eksempel er det digitale oscilloskop U1610A vist ikke i figur 5. Dets båndbredde er 100 MHz, og prisen er næsten 200.000 rubler. Enig, ikke alle har råd til at købe en så dyre enhed.
Figur 5
Lad læseren ikke betragte dette billede som en reklame, da alle sælgers koordinater ikke er malet over: et lignende skærmbillede kunne vises på stedet for dette billede.
Typer af studerede signaler og deres parametre
Den mest almindelige type oscillation i natur og teknologi er en sinusoid. Dette er den samme langmodige funktion Y = sinX, som blev afholdt på skolen i undervisningen i trigonometri. Mange elektriske og mekaniske processer har en sinusform, selvom der ofte bruges andre former for signaler inden for elektronisk teknologi. Nogle af dem er vist i figur 6.
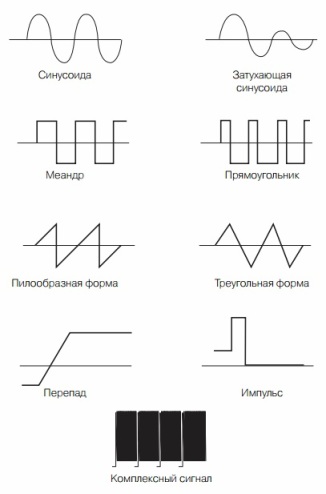
Figur 6. Former af elektriske vibrationer
Periodiske signaler. Signalkarakteristika
Et universelt elektronisk oscilloskop giver dig mulighed for nøjagtigt at studere periodiske signaler. Hvis du på input Y sender et rigtigt lydsignal, for eksempel et musikalsk fonogram, vil tilfældige flimrende burst være synlige på skærmen. Det er naturligvis umuligt at undersøge et sådant signal i detaljer. I dette tilfælde hjælper brugen af et digitalt lagringsoscilloskop, som giver dig mulighed for at gemme bølgeformen.
De i figur 6 viste svingninger er periodiske, gentages efter et vist tidsrum T. Dette kan overvejes mere detaljeret i figur 7.
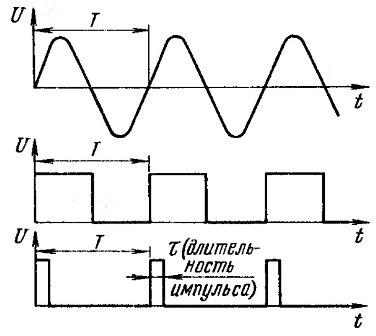
Figur 7. Periodiske udsving
Svingningerne er afbildet i et todimensionalt koordinatsystem: spænding måles langs ordinataksen, og tiden måles langs abscisseaksen. Spænding måles i volt, tid i sekunder. Ved elektriske vibrationer måles tiden ofte i millisekunder eller mikrosekunder.
Foruden komponenter X og Y indeholder bølgeformen også komponent Z - intensitet eller simpelthen lysstyrke (figur 8). Det er hun, der tænder for bjælken for tidspunktet for bjælkens forreste slag og slukker for tidspunktet for tilbagevenden. Nogle oscilloskoper har et input til styring af lysstyrke, der kaldes input Z. Hvis du anvender en pulsspænding fra en referencegenerator til dette input, kan du se frekvensmærker på skærmen. Dette giver dig mulighed for mere målrettet at måle signalets varighed langs X-aksen.
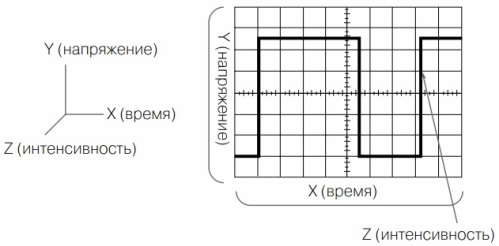
Figur 8. Tre komponenter i det undersøgte signal
Moderne oscilloskoper har som regel tidskalibrerede svejse, der tillader nøjagtig timing. Derfor er det praktisk taget ikke nødvendigt at bruge en ekstern generator til at oprette tags.
Øverst i figur 7 er en sinusbølge. Det er let at se, at det begynder i begyndelsen af koordinatsystemet. I tidsperioden T (periode) udføres en komplet svingning. Så gentages alt, den næste periode. Sådanne signaler kaldes periodiske.
Rektangulære signaler vises under sinusbølgen: bølle og rektangulær puls. De er også periodiske med periode T. Pulslængden betegnes τ (tau). I tilfælde af en krumning er pulsvarigheden τ lig med pausevarigheden mellem impulser, lige halvdelen af perioden T. Derfor er krumningens et specielt tilfælde af en kvadratisk bølge.
Told og told
For at karakterisere rektangulære impulser bruges en parameter kaldet pligtcyklus. Dette er forholdet mellem puls repetitionsperioden T og pulsvarigheden τ. For bugten er driftscyklussen lig med to, - værdien er dimensionløs: S = T / τ.
I engelsk terminologi er det modsatte sandt. Der er impulserne kendetegnet ved driftscyklussen, forholdet mellem impulsvarigheden og perioden for driftscyklussen: D = τ / T. Påfyldningsfaktoren udtrykkes i %%. Dermed er D = 50% for bugten. Det viser sig, at D = 1 / S, driftscyklus og driftscyklus er indbyrdes inverse, selvom de karakteriserer den samme pulsparameter. Bølgeformen af bugten er vist i figur 9.
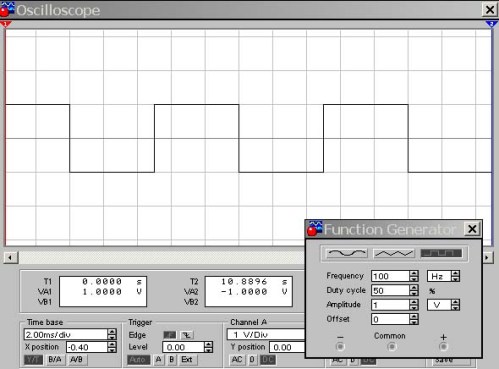
Figur 9. Bølgeform af meander D = 50%
Her er indgangen til oscilloskopet forbundet til udgangen fra den funktionsgenerator, der umiddelbart vises i figurens nederste hjørne. Og her kan en opmærksom læser stille et spørgsmål: “Amplituden af udgangssignalet fra 1V-generatoren, følsomheden for oscilloskopindgangen er 1V / div., Og skærmen viser rektangulære pulser med en styrke på 2V. Hvorfor? "
Faktum er, at den funktionelle generator genererer bipolære rektangulære pulser med hensyn til 0V-niveauet, omtrent det samme som en sinusbølge, med positive og negative amplituder. Derfor observeres pulser med et spændvidde på ± 1V på oscilloskopskærmen. I det følgende figur ændrer vi for eksempel driftscyklussen til 10%.
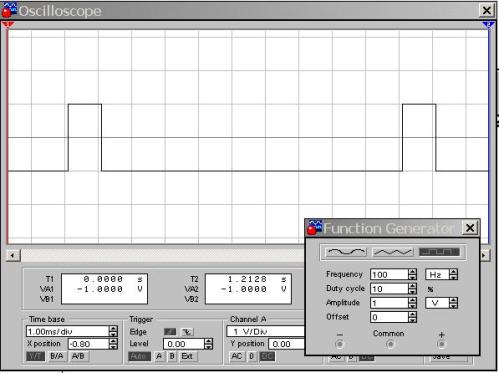
Figur 10. Rektangulær momentum D = 10%
Det er let at se, at repetitionsperioden for puls er 10 celler, mens pulsvarigheden kun er en celle. Derfor er D = 1/10 = 0,1 eller 10%, som det kan ses af generatorens indstillinger. Hvis du bruger formlen til beregning af driftscyklussen, får du S = T / τ = 10/1 = 1 - værdien er dimensionløs. Her kan vi konkludere, at pligtcyklussen karakteriserer impulsen meget mere tydeligt end pligcyklussen.
Faktisk forblev selve signalet det samme som i figur 9: en rektangulær puls med en amplitude på 1 V og en frekvens på 100 Hz. Kun påfyldningsfaktoren eller arbejdscyklussen ændrer sig, det er som om nogen er mere kendt og praktisk. Men for at lette observationen i figur 10 halveres scanningsvarigheden sammenlignet med figur 9 og er 1ms / div. Derfor tager signalperioden 10 celler på skærmen, hvilket gør det forholdsvis let at verificere, at driftscyklussen er 10%. Når du bruger et rigtigt oscilloskop, vælges fejningsvarigheden omtrent den samme.
Rektangulær måling af impulsspænding
Som nævnt i begyndelsen af artiklen måler oscilloskopet spænding, dvs. potentiel forskel mellem to punkter. Målinger foretages typisk i forhold til en fælles ledning, jord (nul volt), selvom dette ikke er nødvendigt. I princippet er det muligt at måle fra minimum til maksimum signalværdier (topværdi, top til top). Under alle omstændigheder er måletrinnene ganske enkle.
Rektangulære pulser er oftest unipolære, hvilket er typisk for digital teknologi. Hvordan man måler spændingen på en rektangulær puls, er vist i figur 11.
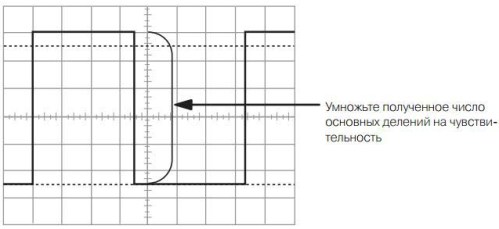
Figur 11. Måling af amplituden af en rektangulær puls
Hvis følsomheden for den lodrette afvigelseskanal er 1V / div, viser det sig, at figuren viser en puls med en spænding på 5,5V. Med en følsomhed på 0,1 V / div. Spændingen vil kun være 0,5 V, selvom begge pulser på skærmen ser nøjagtigt ens.
Hvad andet kan ses i en rektangulær impuls
De rektangulære pulser vist i figur 9, 10 er simpelthen ideelle, fordi de er syntetiseret af Electronics WorkBench. Og pulsfrekvensen er kun 100 Hz, derfor kan der ikke opstå problemer med billedets "kendskab". I en reel anordning, med en høj gentagelsesfrekvens, er pulserne noget forvrængt, først vises forskellige overspændinger og bursts på grund af installationsinduktansen, som vist i figur 12.
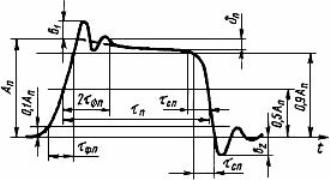
Figur 12. Reel rektangulær impuls
Hvis du ikke er opmærksom på sådanne "bagateller", ser den rektangulære impuls ud som vist i figur 13.
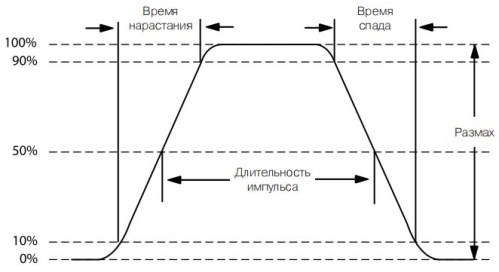
Figur 13. Parametre af en rektangulær puls
Figuren viser, at de forreste og bageste kanter af pulsen ikke vises umiddelbart, men har nogle stignings- og faldtider og er noget skrå i forhold til den lodrette linje. Denne hældning skyldes frekvensegenskaberne for mikrokredsløb og transistorer: jo højere frekvenstransistor, jo mindre “fronter” af pulser. Derfor bestemmes pulsvarigheden af niveauet 50% af det fulde interval.
Af samme grund bestemmes impulsens amplitude af niveauet 10 ... 90%. Impulsvarigheden såvel som spændingen bestemmes ved at multiplicere antallet af opdelinger af den vandrette skala med opdelingsværdien, som vist i figur 14.
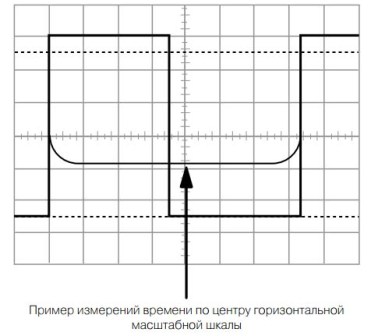
Figur 14
Figuren viser en periode med en rektangulær puls, lidt forskellig fra bugten: varigheden af en positiv puls er 3,5 divisioner af den vandrette skala, og pausevarigheden er 3,8 divisioner. Pulse-gentagelsesperioden er 7,3 divisioner. Et sådant billede kan høre til flere forskellige impulser med forskellige frekvenser. Alt afhænger af fejets varighed.
Antag en scanningsvarighed på 1ms / div. Derefter er puls repetitionsperioden 7,3 * 1 = 7,3ms, hvilket svarer til frekvensen F = 1 / T = 1 / 7.3 = 0.1428KHz eller 143 Hz. Hvis scanningsvarigheden er 1 µs / div, vil frekvensen vise sig at være tusind gange højere, nemlig 143KHZ.
Ved hjælp af dataene i figur 14 er det ikke vanskeligt at beregne pulsens cyklus: S = T / τ = 7.3 / 3.5 = 2.0857, det viser sig næsten som en krumning. Arbejdscyklus pligtcyklus D = τ / T = 3,5 / 7,3 = 0,479 eller 47,9%. Det skal bemærkes, at disse parametre på ingen måde er afhængige af frekvensen: arbejdscyklus og driftscyklus blev beregnet blot ved opdelinger på bølgeformen.
Med rektangulære impulser ser alt ud til at være klart og enkelt. Men vi glemte helt sinusbølgen. Faktisk er den samme ting der: du kan måle spændinger og tidsparametre. En sinusbølgefri periode er vist i figur 15.
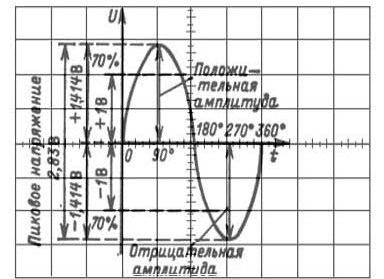
Figur 15. Sine Wave-parametre
For sinusformen vist i figuren er følsomheden af den lodrette afbøjningskanal naturligvis 0,5 V / div. De resterende parametre kan let bestemmes ved at multiplicere antallet af opdelinger med 0,5V / div.
Sinusbølgen kan være en anden, som skal måles med følsomhed, f.eks. 5V / div. I stedet for 1V får du 10V. På skærmen ser billedet af begge sinusoider imidlertid nøjagtigt det samme.
Tidspunktet for den viste sinusoid er ukendt. Hvis vi antager, at scanningsvarigheden er 5ms / div, vil perioden være 20ms, hvilket svarer til en frekvens på 50Hz. Tallene i grader på tidsaksen indikerer sinusoidens fase, selvom dette ikke er særlig vigtigt for en enkelt sinusformet. Oftere er det nødvendigt at bestemme faseskiftet (direkte i millisekunder eller mikrosekunder) mindst mellem to signaler. Dette gøres bedst med et to-strålesoscilloskop. Hvordan dette gøres vises nedenfor.
Sådan måles strøm med et oscilloskop
I nogle tilfælde er det nødvendigt at måle strømens størrelse og form. F.eks. Er vekselstrøm, der strømmer gennem en kondensator, foran spændingen i ¼ periode. Derefter er en modstand med en lille modstand (tiendedele af en Ohm) inkluderet i det åbne kredsløb. En sådan modstand påvirker ikke driften af kredsløbet. Spændingsfaldet over denne modstand viser formen og størrelsen på den strøm, der strømmer gennem kondensatoren.
Et lignende gauge-ammeter er arrangeret på omtrent samme måde, som vil blive inkluderet i brud på det elektriske kredsløb. I dette tilfælde er målemodstanden placeret inde i selve ammeteret.
Kredsløbet til måling af strømmen gennem kondensatoren er vist i figur 16.
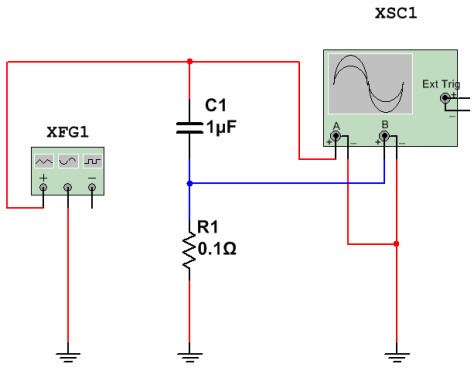
Figur 16. Aktuel måling gennem en kondensator
En sinusformet spænding på 50 Hz med en amplitude på 220 V fra XFG1-generatoren (rød stråle på oscilloskopskærmen) leveres til seriekredsløbet fra kondensatoren C1 og målemodstanden R1. Spændingsfaldet over denne modstand viser formen, fasen og størrelsen på strømmen gennem kondensatoren (blå stråle). Hvordan det ser ud på oscilloskopskærmen vises i figur 17.
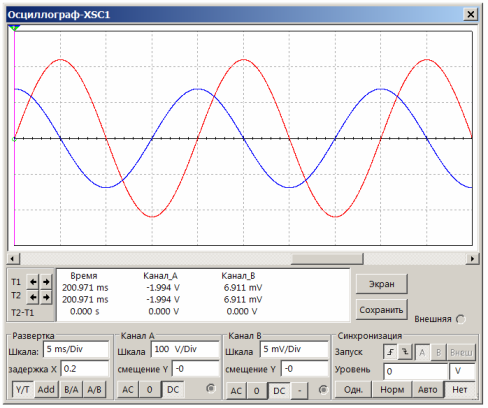
Figur 17. Strømmen gennem kondensatoren ligger foran ¼ periode
Ved en sinusbølgefrekvens på 50 Hz og en scannetid på 5 ms / Div, tager en sinusbølgeperiode 4 opdelinger langs X-aksen, hvilket er meget praktisk til observation. Det er let at se, at den blå stråle ligger foran den røde med nøjagtigt 1 opdeling langs X-aksen, hvilket svarer til ¼ af perioden. Med andre ord er strømmen gennem kondensatoren forud for fasespænding, hvilket er fuldt ud i overensstemmelse med teorien.
For at beregne strømmen gennem kondensatoren er det nok at bruge Ohms lov: I = U / R. Når målemodstanden er 0,1 Ohm, er spændingsfaldet over den 7 mV. Dette er amplitudeværdien. Derefter vil den maksimale strøm gennem kondensatoren være 7 / 0,1 = 70 mA.
Det er ikke meget presserende at måle formen på strømmen gennem kondensatoren, alt er klart og uden målinger. I stedet for en kondensator kan der være enhver belastning: spole, motorvikling, transistorforstærkertrin og meget mere. Det er vigtigt, at denne metode kan bruges til at studere strømmen, som i nogle tilfælde adskiller sig markant i form fra spænding.
Boris Aladyshkin
Se også på elektrohomepro.com
: