kategorier: Udvalgte artikler » Praktisk elektronik
Antal visninger: 32001
Kommentarer til artiklen: 2
Kondensatorer i elektroniske kredsløb
I tidligere artikler talte vi kort om driften af kondensatorer i vekslingskredsløb, hvordan og hvorfor kondensatorer passerer vekselstrøm (se - AC kondensatorer). I dette tilfælde opvarmes ikke kondensatorerne, der tildeles ikke strøm til dem: i den ene halvbølge af sinusformen oplades kondensatoren, og i den anden tømmes den naturligt ud, mens den lagrede energi overføres til den aktuelle kilde.
Denne metode til at føre strøm giver dig mulighed for at kalde kondensatoren en fri modstand, og det er derfor, kondensatoren, der er tilsluttet udløbet, ikke får tælleren til at dreje. Og alt dette skyldes, at strømmen i kondensatoren ligger foran nøjagtigt 1/4 af den tid, den spænding, der påføres den.
Men denne faseudvikling tillader ikke kun at "narre" tælleren, men gør det også muligt at oprette forskellige kredsløb, for eksempel generatorer af sinusformede og rektangulære signaler, tidsforsinkelser og forskellige frekvensfiltre.
I processen med denne historie bliver man undertiden nødt til at huske, hvad der allerede er blevet sagt før, så at sige, for at opsummere. Dette vil hjælpe med ikke at vende tilbage til tidligere artikler for at huske en simpel formel, eller simpelthen "hvad er det?"
Parallel- og serieforbindelse af kondensatorer
Med en parallel forbindelse af kondensatorer er den samlede kapacitet simpelthen den aritmetiske sum af kapaciteterne. Naturligvis, med denne inkludering, vil den samlede kapacitans være større end kapaciteten til den største kondensator. Ctotal = C1 + C2 + C3 + ... + Cn.
I tilfælde af en serieforbindelse er den samlede kapacitet mindre end den mindste.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Når to identiske kondensatorer er forbundet i serie, vil den totale kapacitans være lig med halvdelen af kapacitansen for en: for eksempel, når to kondensatorer tilsluttes på hver 1 µF, vil den samlede kapacitans være 0,5 µF.
Kapacitans Xc
Her er alt som ved tilslutning af modstande kun det nøjagtige modsætning: en serieforbindelse reducerer den totale kapacitans, og en parallel forøger den. Denne situation bør ikke glemmes, når kondensatorer forbindes, da en stigning i kapacitansen fører til et fald i kapaciteten Xc
Xc = 1/2 * π * f * C.
Fra matematikens synspunkt er dette ganske naturligt, fordi kapaciteten C er i nævneren af fraktionen. Forresten er frekvensen f det samme sted, så en stigning i frekvensen fører også til et fald i kapaciteten Xc. Den fysiske betydning af dette er, at det gennem den samme kondensator er bedre, mere uhindret, at høje frekvenser passerer. Dette vil blive drøftet lidt senere, når det kommer til lavpas- og højpasfiltrene.
Hvis vi tager en kondensator med en kapacitet på 1 μF, vil Xc for en frekvens på 60 Hz være 2653 ohm, og for en frekvens på 400 Hz har den samme kondensator en Xc på kun 398 ohm. De, der ønsker det, kan kontrollere disse resultater med formlen ved at erstatte π = 3,14, frekvensen i hertz og kapacitansen i farads. Så vil resultatet være i ohm. Alt skal overholde SI-systemet!
Men kondensatorer bruges ikke kun som fritdæmpende dæmpningsmodstand eller i ensretterfiltre. Uden deres deltagelse, kredsløb til lav- og højfrekvensgeneratorer, forskellige bølgeformkonvertere, differentierende og integrerende kredsløb, forstærkere og andre ordninger.
Dernæst overvejes forskellige elektriske signaler, som kondensatorerne skal arbejde med. Først og fremmest er dette periodiske signaler, der er egnede til observation med oscilloskop.
Periode og frekvens af svingninger
En periodisk svingning kaldes derfor periodisk, som uden ophør gentager den samme form, for eksempel en sinusformet svingning. Varigheden af denne fulde sving kaldes nøjagtigt perioden T og måles i sekunder, millisekunder, mikrosekunder.Moderne elektronik beskæftiger sig endda med nanosekunder (en milliardedels sekund).
Antallet af perioder pr. Sekund kaldes frekvensen (hvor ofte) af svingningerne f og udtrykkes i hertz. 1Hz er den frekvens, hvorpå en svingning, en hel periode, udføres på 1 sekund. Forholdet mellem periode og frekvens udtrykkes med den enkle formel T = 1 / f.
Når man kender oscilleringsperioden, er det derfor meget simpelt at beregne frekvensen f = 1 / T.
Sådan beregnes frekvensen, når man måler med et oscilloskop: antallet af celler i en periode beregnes, ganget med varigheden af en celle, og perioden opnås for eksempel i mikrosekunder. Og for at finde ud af hyppigheden brugte de simpelthen den sidste formel.
almindelig elektronisk oscilloskop Lader dig kun observere periodiske signaler, der kan synkroniseres med fejefrekvensen for at få et stillbillede, der er egnet til forskning. Hvis signalet fra et musikprogram sendes til indgangen til oscilloskopet, vil du ikke være i stand til at stoppe billedet for noget. For at observere sådanne signaler bruges lagringsoscilloskoper.
Når en periode måles i millisekunder, opnås frekvensen i kilohertz, i en periode målt i mikrosekunder, udtrykkes frekvensen allerede i megahertz. Dette er, hvis du ikke følger kravene i SI-systemet: periode i sekunder, frekvens i hertz.
Ikke-sinusformede vibrationer
Som nævnt tidligere er en sinusbølge den mest almindelige og egnede til undersøgelse og praktisk anvendelse af den periodiske kurve. Under industrielle forhold opnås det ved hjælp af elektriske generatorer, for eksempel i vandkraftværker. I elektroniske enheder bruges vibrationer med de mest forskellige former.
Grundlæggende er dette tre former: sinusformet, rektangulært og trekantet, som vist i figur 1. Både strøm og spænding kan have en sådan form, derfor er kun tidsaksen vist på figuren, ordinataksen står uden navn.
Sådanne svingninger genereres af specielle elektroniske kredsløb. Rektangulære og trekantede signaler kaldes ofte pulserende. Der er imidlertid en masse elektroniske kredsløb, der udfører signalkonvertering: for eksempel et rektangel, en trekant kan laves af en sinusform.
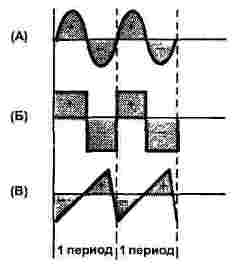
Figur 1
For alle tre signaler viser figuren to perioder, alle signaler har den samme frekvens.
Spektrum af ikke-sinusformede signaler
Ethvert elektrisk signal kan repræsenteres som en måling af amplituden på et tidspunkt. Hyppigheden af disse prøver kaldes samplingfrekvensen og mindst to gange højere end den øvre frekvens af det målte signal. Fra disse prøver kan du derefter gendanne det originale signal. Denne metode bruges f.eks. I digital lydoptagelse. Denne metode kaldes også tidsanalyse.
En anden metode antager, at ethvert signal, endda et rektangulært signal, kan repræsenteres som den algebraiske sum af sinusoider med forskellige frekvenser og faser. Denne metode kaldes frekvensanalyse. Men hvad der blev sagt "med forskellige frekvenser" er ikke helt sandt: de indholdende sinusoider kaldes harmoniske og deres frekvenser overholder visse love.
En sinusbølge, hvis frekvens er lig med en kvadratbølges frekvens kaldes den grundlæggende eller første harmoniske. Selv harmoniske egenskaber opnås ved at multiplicere den grundlæggende frekvens med henholdsvis et lige antal og ulige harmoniske med ulige.
Så hvis den første harmoniske har en frekvens på 1000 Hz, er den anden 2000 Hz, den fjerde er 4000 Hz osv. Mærkelige harmoniske har frekvenser på 3000Hz, 5000Hz. Desuden er hver harmonisk mindre i amplitude end den vigtigste: jo højere den harmoniske, desto mindre er amplituden.
I musik kaldes harmoniske overtoner. Det er dem, der danner lydklang, gør det muligt at skelne violin fra klaver og guitar fra saxofon. De tillader ikke at forvirre den mandlige og kvindelige stemme eller at skelne Petrov fra Ivanov. Og kun sinusformen i sig selv kan ikke længere nedbrydes eller samles fra nogen signaler.
Figur 2 viser konstruktionen af en rektangulær puls.
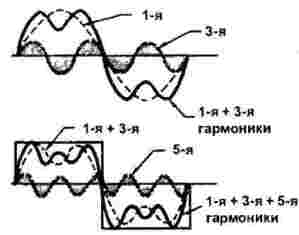
Figur 2
Den første og tredje harmonik vises i den øverste del af figuren. Det er let at se, at i en periode af den første harmoniske tre perioder af tredje pass. I dette tilfælde er amplituden af den tredje harmoniske en tredjedel af den første. Summen af den første og den tredje harmonik vises også her.
Nedenfor vises sammen med summen af 1 og 3 harmoniske yderligere 5 harmoniske: for en periode med et rektangulært signal formår det at udføre nøjagtigt fem perioder. I dette tilfælde er dens amplitude endnu mindre, mere præcist, nøjagtigt 1/5 af den vigtigste (første). Men man skal ikke tro, at alt ender på den femte harmoni: i figuren er det bare ikke muligt at vise alt, faktisk er der meget mere.
Dannelsen af savtand og trekantede signaler, der er vist i figur 3., er noget mere kompliceret. Hvis i forrige tilfælde kun ulige harmoniske deltog, kommer endda harmoniske ind i spillet.
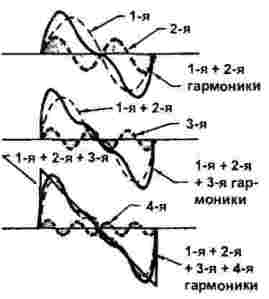
Figur 3
Således kan vi konstatere det faktum, at ved hjælp af mange harmonikker syntetiseres et signal af enhver form, og antallet og typen af harmoniske afhænger af bølgeformen, som vist i figur 2 og 3.
Ved reparation og installation af elektronisk udstyr bruges et oscilloskop til undersøgelse af elektriske signaler. Det giver dig mulighed for at overveje formen af periodiske signaler, deres amplitude, måle gentagelsesperioden. Men de harmonier, der er vist i figur 2 og 3, kan ikke ses.
Selv hvis du f.eks. Forbinder en elektrisk guitar til et oscilloskop, trækker en streng, vises en sinus på skærmen, det er den første harmoniske. I dette tilfælde kan der ikke være tale om overtoner. Den samme sinusoid vil resultere, hvis du blæser ind i røret eller fløjten foran mikrofonen.
Sådan får du rektangulære impulser
Når vi har kendt elektriske signaler, skal vi huske de kondensatorer, som artiklen begyndte med. Først og fremmest skal du blive bekendt med en af de klassiske elektronik kredsløb - mULTIVIBRATOR, (Figur 4) det er han, der genererer rektangulære pulser. Kredsløbet er så klassisk, at det begynder at arbejde med det samme uden at kræve indstillinger eller justeringer.
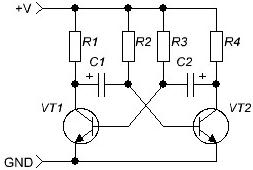
Figur 4
Multivibratoren er en totrinsforstærker, der er dækket af positiv feedback. Hvis kollektorbelastningsmodstandene R1 = R4, basismodstanderne R2 = R3 og kondensatorerne C1 = C2 er ens, kaldes multivibratoren symmetrisk og genererer kvadratiske bølgepulser af slingertypen - pulsvarigheden er lig med pausevarigheden.
Pulscyklussen for sådanne pulser (forholdet mellem perioden og pulsvarigheden) er lig med to. I engelsksprogede ordninger er alt nøjagtigt det modsatte: De kalder det pligtcyklus. Det beregnes som forholdet mellem impulsvarigheden og perioden for dens succession og udtrykkes som en procentdel. Således er driftscyklussen for meanderne 50%.
Er computeren korrekt?
Navnet multivibrator blev foreslået af den hollandske fysiker van der Pol, da spektret af et rektangulært signal indeholder mange harmonier. Du kan bekræfte dette, hvis du kan placere en radiomodtager, der fungerer i mellembølgerområdet i nærheden af en multivibrator, der fungerer selv ved en lydfrekvens: howls kommer fra højttaleren. Dette antyder, at ud over lydfrekvens udsender multivibratoren også højfrekvente svingninger.
For at bestemme genereringsfrekvensen kan man bruge formlen f = 700 / (C1 * R2).
Med denne formel med formlen, kondensatoren i mikrofaradene (μF), modstanden i kilo-ohm (KΩ), resultatet i hertz (Hz). Frekvensen bestemmes således af tidskonstanten for C1 * R2-kredsløbet; samlerbelastninger påvirker ikke frekvensen. Hvis vi tager C1 = 0,02 μF, R2 = 39 KΩ, får vi f = 700 / (0,02 * 39) = 897,4 Hz.
Multivibrator i computerenes alder og mikrocontrollere I henhold til dette skema bruges det næsten aldrig, skønt det meget vel kan være egnet til forskellige eksperimenter. Først og fremmest ved hjælp af computere. Sådan ser multivibrator-kredsløbet samlet i Multisim-programmet ud. Det viser også forbindelsen til oscilloskopet.
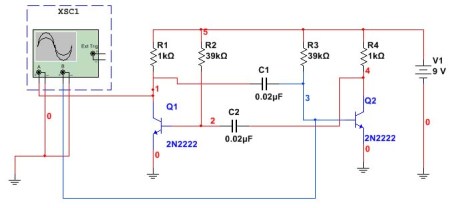
Figur 5
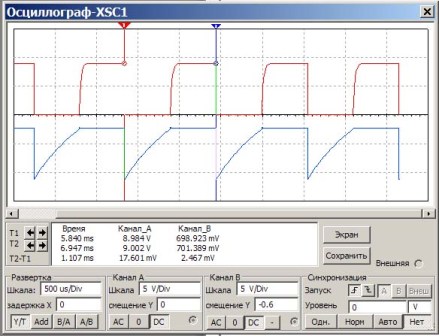
I dette kredsløb er kondensatorer og modstande installeret som i det foregående eksempel. Opgaven er at kontrollere beregningen i henhold til formlen, om den samme frekvens opnås. For at gøre dette skal du måle pulsenes periode og derefter beregne dem i frekvens. Resultatet af Multisim-oscilloskopet er vist i figur 6.
Figur 6
Nogle afklaringer til figur 6.
På oscilloskopskærmen viser den røde puls impulser på transistoropsamleren og den blå på baserne. Under skærmen i et stort hvidt vindue viser tallene måleresultaterne. Vi er interesseret i kolonnen "Tid". Tiden måles ved indikatorerne T1 og T2 (røde og blå trekanter over skærmen).
Således er puls repetitionsperioden T2-T1 = 1.107ms vist ganske nøjagtigt. Det gjenstår kun at beregne frekvensen f = 1 / T = 1 / 1,107 * 1000 = 903Hz.
Resultatet er næsten det samme som i beregningen i henhold til formlen, der gives lidt højere.
Kondensatorer kan ikke kun bruges separat: i kombination med modstande giver de dig mulighed for blot at oprette forskellige filtre eller oprette faseskiftkredsløb. Men dette vil blive drøftet i den næste artikel.
Fortsættelse af artiklen: Kondensatorer i elektroniske kredsløb. Del 2
Boris Aladyshkin
Se også på elektrohomepro.com
: