Hvad er effektiv, rms, effektiv spænding eller strøm?

Gennemsnitsværdi af vekslende sinusformet spænding eller strøm

Når man taler om en værdi, der varierer i henhold til en sinusformet (harmonisk) lov, er det muligt at bestemme dens gennemsnitlige værdi over halve perioden. Da strømmen i netværket i vores store flertal af tilfælde er sinusformet, for dens nuværende kan dens gennemsnitsværdi (i halve perioden) også let findes, er det nok at ty til integrationsoperationen og sætte grænserne fra 0 til T / 2. Som et resultat får vi:

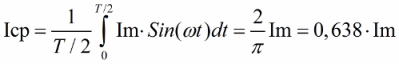
Ved at erstatte Pi = 3,14 finder vi den gennemsnitlige værdi af sinusstrømmen over halvdelen af ​​perioden afhængigt af dens amplitude. Tilsvarende findes den gennemsnitlige værdi af sinusformet EMF eller sinusformet spænding U:

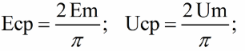
Effektiv værdi af strøm I eller spænding U

Imidlertid er gennemsnitsværdien ikke så vidt brugt i praksis som den effektive værdi af en sinusformet strøm eller spænding. Den effektive værdi af en værdi, der sinusformerer i tid, er den gennemsnitlige firkantede værdi, med andre ord dens effektive værdi.

Den effektive (eller effektive) værdi af strømmen eller spændingen findes på samme måde ved integration, men med hensyn til firkanterne og med den efterfølgende ekstraktion af kvadratroten og grænserne for integration er nu en hel periode med sinusformet funktion.

Så for den nuværende vil vi have:

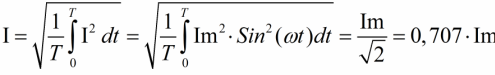
Ved at udskifte rodværdien på 2 får vi en formel til at finde den effektive (effektive, rms) værdi af strøm, spænding, EMF - i forhold til amplitudeværdien. Denne formel kan findes meget ofte, den bruges overalt i beregningerne forbundet med vekslende sinusformede strømkredsløb:

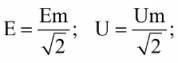
Fra et praktisk synspunkt, hvis vi sammenligner den termiske virkning af en vekslende sinusformet strøm med den termiske virkning af en kontinuerlig kontinuerlig strøm over det samme tidsrum på den samme aktive belastning, viser det sig, at den varme, der frigives i perioden med sinusformet vekselstrøm, er lig med den tildelte i løbet af samme tid varmen fra jævnstrømmen, forudsat at jævnstrømmen vil være mindre end amplituden af ​​vekselstrømmen til roden af ​​2 gange:

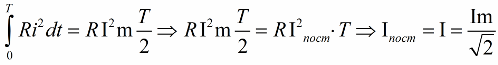
Dette betyder, at den effektive (effektive, rms) værdi af sinusformet vekselstrøm er numerisk lig med værdien af ​​den jævnstrøm, ved hvilken den termiske virkning (udsendt varmemængde) af denne jævnstrøm på den aktive modstand i en periode af sinusformen er lig med den termiske virkning af denne sinusformede strøm i samme periode .

Tilsvarende findes den effektive (effektive, rms) værdi af sinusformet spænding eller sinusformet EMF.

Langt de fleste moderne bærbare måleinstrumenterNår man måler vekselstrøm eller vekslingsspænding, viser de nøjagtigt den effektive værdi af den målte mængde, dvs. rms-værdien, og ikke dens amplitude og ikke gennemsnitsværdien over en halv periode.

Hvis der ikke er andre afklarende indstillinger på enheden, men der er et ~ I eller ~ U-ikon, måles de aktuelle værdier for strøm og spænding. Betegnelser for en bestemt amplitude eller en bestemt betjeningsenhed er Im (m - maksimum - maksimum, amplitude) eller Irms (rms - Root Mean Square - rms værdi).