AC kondensatorer

Hvad er vekselstrøm?

Hvis vi overvejer en jævn strøm, kan den ikke altid være perfekt konstant: spændingen ved kildeudgang kan afhænge af belastningen eller af graden af ​​udladning af batteriet eller det galvaniske batteri. Selv med en konstant stabiliseret spænding afhænger strømmen i det eksterne kredsløb af belastningen, hvilket bekræfter Ohms lov. Det viser sig, at dette heller ikke er helt konstant strøm, men en sådan strøm kan heller ikke kaldes variabel, da den ikke ændrer retning.

En variabel kaldes normalt spænding eller strøm, hvis retning og styrke ikke ændres under påvirkning af eksterne faktorer, såsom en belastning, men er helt "uafhængig": det er sådan generatoren genererer den. Derudover skal disse ændringer være periodiske, dvs. gentagelse over en bestemt periode kaldet en periode.

Hvis spændingen eller strømmen på nogen måde ændrer sig, uden at bekymre sig om frekvensen og andre regelmæssigheder, kaldes et sådant signal støj. Et klassisk eksempel er "sne" på en tv-skærm med et svagt transmissionssignal. Eksempler på nogle periodiske elektriske signaler er vist i figur 1.

For jævnstrøm er der kun to karakteristika: polariteten og spændingen for kilden. I tilfælde af vekselstrøm er disse to mængder helt klart ikke nok, så der vises flere flere parametre: amplitude, frekvens, periode, fase, øjeblikkelig og effektiv værdi.

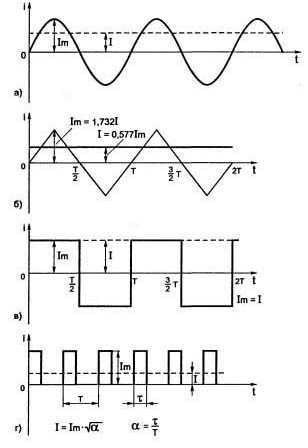
Figur 1Eksempler på nogle periodiske elektriske signaler

Oftest inden for teknologi har man at gøre med sinusformede svingninger, derudover ikke kun inden for elektroteknik. Forestil dig et bilhjul. Når man kører ensartet på en god glat vej, beskriver hjulets centrum en lige linje parallelt med vejoverfladen. Samtidig bevæger ethvert punkt på hjulets periferi langs en sinusform i forhold til den netop nævnte linje.

Ovennævnte kan bekræftes ved figur 2, der viser en grafisk metode til konstruktion af en sinusformet: den, der studerede tegning, ved, hvordan man udfører sådanne konstruktioner.

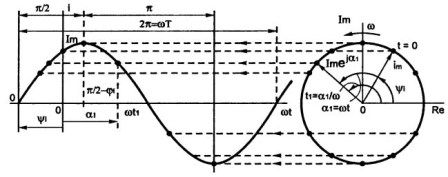
Figur 2Grafisk sinebølgemetode

Fra fysikskolen er det kendt, at en sinus er den mest almindelige og egnede til at studere en periodisk kurve. På nøjagtig samme måde opnås sinusformede svingninger i generatorerpå grund af deres mekaniske enhed.

Figur 3 viser en graf over sinusformet strøm.

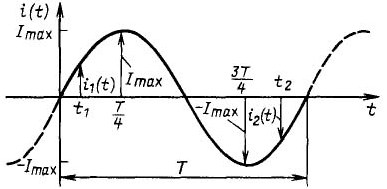
Figur 3Sinusformet nuværende graf

Det er let at se, at strømstyrken varierer med tiden, derfor er ordinataksen angivet i figuren som i (t), er funktionen af ​​strøm kontra tid. Den fulde periode med strømmen er angivet med en solid linje og har en periode T. Hvis du starter overvejelsen fra oprindelsen, kan du se, at først strømmen stiger, når Imax, går gennem nul, falder til –Imax og derefter øges og når nul. Dernæst begynder den næste periode som vist med den stiplede linje.

I form af en matematisk formel skrives den aktuelle adfærd som følger: i (t) = Imax * sin (ω * t ± φ).

Her i (t) er den øjeblikkelige værdi af strømmen, afhængigt af tid, Imax er amplitudeværdien (maksimal afvigelse fra ligevægtstilstanden), ω er den cirkulære frekvens (2 * π * f), φ er fasevinklen.

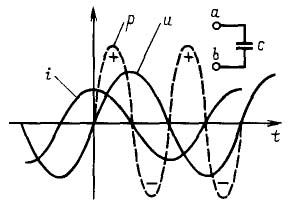
Cirkelfrekvensen ω måles i radianer pr. Sekund, og fasevinklen φ i radianer eller grader. Sidstnævnte giver kun mening, når der er to sinusformede strømme. For eksempel i kæder med kondensator strømmen er foran spændingen 90˚ eller nøjagtigt en fjerdedel af perioden, som vist i figur 4. Hvis der er en sinusformet strøm, kan du flytte den langs ordinataksen, som du vil, og intet vil ændre sig fra dette.

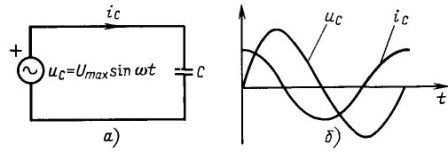
Figur 4 I kredsløb med en kondensator er strømmen foran spændingen et kvarter

Den fysiske betydning af cirkelfrekvensen ω er, hvilken vinkel i radianer vil "løbe gennem" en sinusoid på et sekund.

Periode - T er det tidspunkt, i hvilket sinusbølgen foretager en komplet svingning. Det samme gælder vibrationer med en anden form, for eksempel rektangulær eller trekantet. Perioden måles i sekunder eller mindre enheder: millisekunder, mikrosekunder eller nanosekunder.

En anden parameter for ethvert periodisk signal, inklusive en sinus, er hyppigheden, hvor mange svingninger signalet vil gøre på 1 sekund. Måleenheden for frekvens er Hertz (Hz), opkaldt efter det 19. århundrede forsker Heinrich Hertz. Så frekvensen på 1 Hz er intet mere end en svingning / sekund. F.eks. Er lysnettets frekvens 50Hz, det vil sige, at nøjagtigt 50 sinusformede perioder går på et sekund.

Hvis den aktuelle periode er kendt (du kan måle med et oscilloskop), så vil frekvensen af ​​signalet hjælpe med at finde ud af formlen: f = 1 / T. Hvis tiden udtrykkes i sekunder, vil resultatet desuden være i Hertz. Omvendt er T = 1 / f, frekvens i Hz, tiden opnås i sekunder. For eksempel, hvornår 50 hertz perioden vil være 1/50 = 0,02 sekunder eller 20 millisekunder. I elektricitet bruges oftere højere frekvenser: KHz - kilohertz, MHz - megahertz (tusinder og millioner af svingninger pr. Sekund) osv.

Alt, hvad der er sagt for strøm, er også sandt for vekslende spænding: i figur 6 er det nok at blot ændre bogstavet I til U. Formlen vil se sådan ud: u (t) = Umax * sin (ω * t ± φ).

Disse forklaringer er nok til at vende tilbage til eksperimentere med kondensatorer og forklar deres fysiske betydning.

Kondensatoren leder vekselstrøm, som blev vist på diagrammet i figur 3 (se artikel - Kondensatorer til AC elektriske installationer). Lampens lysstyrke øges, når der tilsluttes en ekstra kondensator. Når kondensatorerne er parallelt tilsluttet, tilføjes deres kapaciteter ganske enkelt, så det kan antages, at kapacitansen Xc afhænger af kapacitansen. Derudover afhænger det også af frekvensen af ​​strømmen, og derfor ser formlen sådan ud: Xc = 1/2 * π * f * C.

Det følger af formlen, at med stigende kapacitans og frekvens af vekslingsspændingen falder reaktansen Xc. Disse afhængigheder er vist i figur 5.

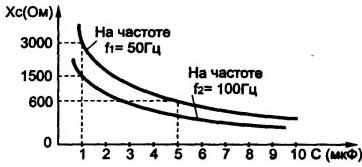
Figur 5. Afhængigheden af ​​kondensatorens reaktans af kapacitansen

Hvis vi erstatter frekvensen i Hertz med formlen og kapacitansen i Farads, vil resultatet være i Ohms.

Vil kondensatoren varme op?

Husk nu oplevelsen med en kondensator og en elektrisk måler, hvorfor roterer den ikke? Faktum er, at måleren overvejer aktiv energi, når forbrugeren er en rent aktiv belastning, for eksempel glødelamper, en elkedel eller en elektrisk komfur. For sådanne forbrugere, spænding og strøm falder sammen i fase, har et tegn: Hvis du multiplicerer to negative tal (spænding og strøm under den negative halvcyklus), er resultatet i henhold til matematikloverne stadig positivt. Derfor er sådanne forbrugers kapacitet altid positiv, dvs. går ind i belastningen og frigøres i form af varme, som vist i figur 6 med den stiplede linje.

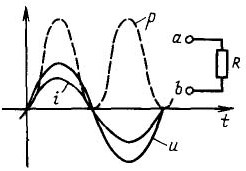
Figur 6

I tilfælde, hvor kondensatoren er inkluderet i vekselstrømskredsløbet, falder strømmen og spændingen ikke i fase: strømmen er 90 оп foran fase i spænding, hvilket fører til en kombination, når strømmen og spændingen har forskellige tegn.

Figur 7

I disse øjeblikke er kraften negativ. Med andre ord, når kraften er positiv, lades kondensatoren, og når den er negativ, overføres den lagrede energi tilbage til kilden. Derfor viser det sig i gennemsnit med nuller, og der er simpelthen ikke noget at tælle her.

Kondensatoren opvarmes slet ikke engang, medmindre den selvfølgelig kan betjenes. Derfor ofte kondensator kaldet fri modstand, som tillader det at bruge i transformerfri strømforsyning med lav effekt.Selvom sådanne blokke ikke anbefales på grund af deres fare, er det stadig nogle gange nødvendigt at gøre dette.

Før installation i en sådan enhed slukke kondensator, skal det kontrolleres ved simpel forbindelse til netværket: hvis kondensatoren ikke er opvarmet i en halv time, kan den med sikkerhed inkluderes i kredsløbet. Ellers er du bare nødt til at smide den væk uden beklagelse.

Hvad viser et voltmeter?

Ved fremstilling og reparation af forskellige enheder, skønt ikke så ofte, er det nødvendigt at måle vekslende spændinger og endda strømme. Hvis en sinusoid opfører sig så hektisk, så op og ned, hvad viser et normalt voltmeter?

Den gennemsnitlige værdi af et periodisk signal, i dette tilfælde en sinusform, beregnes som det område, der er afgrænset af abscissa-aksen og det grafiske billede af signalet divideret med 2 * π radianer eller sinusoidens periode. Da de øvre og nedre dele er absolut identiske, men har forskellige tegn, er den gennemsnitlige værdi af sinusformen nul, og det er ikke nødvendigt at måle det overhovedet, og det er endda simpelthen meningsløst.

Derfor viser måleenheden os rms-værdien af ​​spændingen eller strømmen. Den gennemsnitlige kvadratværdi er en sådan værdi af den periodiske strøm, hvor den samme mængde varme frigøres på den samme belastning som ved lige strøm. Med andre ord lyser pæren med den samme lysstyrke.

Dette beskrives med formlerne som dette: Icr = 0,707 * Imax = Imax / √2 for spænding, formlen er den samme, bare skift et bogstav Ucr = 0.707 * Umax = Umax / √2. Det er disse værdier, som måleenheden viser. De kan erstattes med formler, når de beregnes i henhold til Ohms lov eller ved beregning af effekt.

Men dette er ikke alt, hvad en kondensator i et vekselstrømsnetværk er i stand til. I den næste artikel vil vi overveje brugen af ​​kondensatorer i pulserede kredsløb, højpas- og lavpasfiltre i sinusbølger og firkantbølgeneratorer.

Boris Aladyshkin

Fortsættelse af artiklen: Kondensatorer i elektroniske kredsløb

Comments

[#1]

Artiklen er god. Kognitiv, figur 7, vil jeg tilføje, at dielektrikeren opvarmes i kondensatorerne på grund af dens polarisering. Jeg vil stille et spørgsmål til forfatteren. Det er ikke klart, hvorfor når der ikke er nogen spænding på kondensatoren, der ikke er nogen potentialeforskel på pladerne, strømmer den maksimale strøm gennem kondensatoren.