Hvad er en PID-controller?

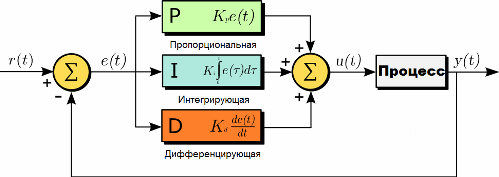
PID (fra det engelske P-proportional, I-integreret, D-derivat) - en regulator er en enhed der bruges i kontrolsløjfer udstyret med et feedbacklink. Disse controllere bruges til at generere et styresignal i automatiske systemer, hvor det er nødvendigt at opnå høje krav til transienternes kvalitet og nøjagtighed.

PID-regulatorens styresignal opnås ved at tilføje tre komponenter: den første er proportional med værdien af ​​fejlsignalet, den anden er integralen af ​​fejlsignalet, og den tredje er dens derivat. Hvis nogen af ​​disse tre komponenter ikke er inkluderet i tilføjelsesprocessen, vil controlleren ikke længere være PID, men blot proportional, proportionalt differentierende eller proportionalt integreret.

Den første komponent er proportional

Udgangssignalet giver en proportional komponent. Dette signal fører til modregning til den aktuelle afvigelse af den indgangsmængde, der skal reguleres fra den indstillede værdi. Jo større afvigelse, jo større er signalet. Når værdien af ​​den kontrollerede variabel er lig med den indstillede værdi ved indgangen, bliver udgangssignalet lig med nul.

Hvis vi kun forlader denne proportionelle komponent og kun bruger den, stabiliseres værdien af ​​den mængde, der skal reguleres, aldrig til den korrekte værdi. Der er altid en statisk fejl, der er lig med en sådan værdi af afvigelsen af ​​den kontrollerede variabel, at udgangssignalet stabiliseres ved denne værdi.

For eksempel styrer en termostat strømmen til en varmeenhed. Udgangssignalet falder, når den ønskede objekttemperatur nærmer sig, og styresignalet stabiliserer effekten på niveauet for varmetab. Som et resultat når den indstillede værdi ikke den indstillede værdi, fordi varmeenheden bare skal slukkes og begynder at køle ned (strømmen er nul).

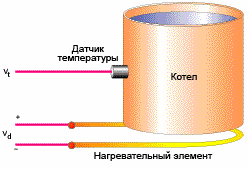
Forstærkningen mellem input og output er større - den statiske fejl er mindre, men hvis forstærkningen (faktisk proportionalitetskoefficienten) er for stor, så udsættes der for forsinkelser i systemet (og de er ofte uundgåelige), begynder selvsvingninger snart i det, og hvis du øger koefficienten er endnu større - systemet mister simpelthen stabiliteten.

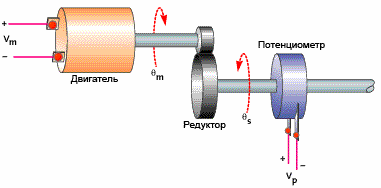
Eller et eksempel på placering af en motor med en gearkasse. Med en lille koefficient nås den ønskede position af arbejdsorganet for langsomt. Forøg koefficienten - reaktionen vil være hurtigere. Men hvis du øger koefficienten yderligere, vil motoren "flyve over" til den rigtige position, og systemet bevæger sig ikke hurtigt til den ønskede position, som man kunne forvente. Hvis vi nu øger proportionalitetskoefficienten yderligere, vil svingninger begynde i nærheden af ​​det ønskede punkt - resultatet opnås ikke igen ...

Den anden komponent er integrering

Tidsintegralet af uoverensstemmelsen er hoveddelen af ​​den integrerende komponent. Det er proportional med dette integral. Den integrerende komponent bruges bare til at eliminere den statiske fejl, da controlleren over tid tager højde for den statiske fejl.

I fravær af eksterne forstyrrelser vil den værdi, der skal reguleres, efter nogen tid stabiliseres til den korrekte værdi, når den forholdsmæssige komponent viser sig at være nul, og outputens nøjagtighed garanteres fuldstændigt af den integrerende komponent. Men den integrerende komponent kan også generere svingninger i nærheden af ​​positioneringspunktet, hvis koefficienten ikke er valgt korrekt.

Den tredje komponent er differentierende

Ændringshastigheden for afvigelsen af ​​den mængde, der skal reguleres, er proportional med den tredje, den differentierende komponent.Det er nødvendigt for at modvirke afvigelser (forårsaget af eksterne påvirkninger eller forsinkelser) fra den korrekte position, der er forudsagt i fremtiden.

PID Controller Theory

Som du allerede har forstået, bruges PID-controllere til at opretholde en given værdi x0 af en bestemt mængde på grund af en ændring i værdien af ​​u for en anden mængde. Der er et sætpoint eller en given værdi x0, og der er en forskel eller uoverensstemmelse (mismatch) e = x0-x. Hvis systemet er lineært og stationært (praktisk talt er dette næppe muligt), er følgende formler for definitionen af ​​u gyldige:

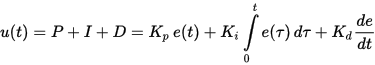
I denne formel ser du proportionalitetskoefficienterne for hver af de tre udtryk.

I praksis bruger PID-controllere en anden formel til tuning, hvor forstærkningen anvendes umiddelbart på alle komponenter:

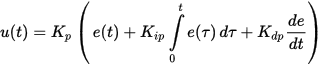
Den praktiske side af PID-kontrol

Praktisk teoretisk analyse af PID-kontrollerede systemer anvendes sjældent. Problemet er, at kontrolobjektets egenskaber er ukendte, og systemet er næsten altid ustabilt og ikke-lineært.

Faktisk fungerende PID-controllere har altid en begrænsning af driftsområdet nedenfor og ovenover, hvilket grundlæggende forklarer deres ikke-linearitet. Derfor er tuning næsten altid og overalt udført eksperimentelt, når kontrolobjektet er tilsluttet styresystemet.

Brug af værdien genereret af softwarekontrolalgoritmen har et antal specifikke nuancer. Hvis det f.eks. Drejer sig om temperaturregulering, er det ofte nødvendigt ikke kun en, men to enheder på én gang: den første styrer opvarmning, den anden styrer køling. Den første leverer det opvarmede kølevæske, det andet - kølemediet. Tre muligheder for praktiske løsninger kan overvejes.

Den første er tæt på den teoretiske beskrivelse, når output er en analog og kontinuerlig mængde. Det andet er et output i form af et sæt pulser, for eksempel til styring af en trinmotor. Tredje - PWM-kontrolnår output fra regulatoren tjener til at indstille pulsbredden.

I dag er næsten alle automatiseringssystemer under konstruktion baseret på PLC, og PID-controllere er specielle moduler, der føjes til styreenheden eller generelt implementeres programmatisk ved indlæsning af biblioteker. For korrekt at indstille gevinsten i sådanne controllere leverer deres udviklere speciel software.