Boolsk algebra. Del 1. Lidt af historien

I skolen studerede vi alle algebra, men de talte ikke om boolsk algebra der. Hvad er forskellen mellem boolsk algebra og skolealgebra, historien om dens udseende, problemer og anvendelser er beskrevet i denne artikel.

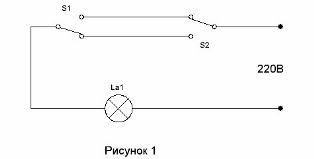
Kredsløbet, der giver to afbrydere mulighed for at tænde lyset i korridoren ved indgangen til korridoren og slukke for det, når man kommer ind i rummet, har været kendt i meget lang tid (se. Korridor belysning kontrol kredsløb). Det er vist i figur 1.

Opgave nummer 1. Mere kompliceret. Opret et diagram, der giver dig mulighed for at tænde og slukke for lyset i dit værelse med en af ​​tre forskellige afbrydere. Kontakterne er placeret ved indgangen til rummet, over sengen og ved skrivebordet.

Opgave nummer 2.

I et sportsudvalg, såsom et fabrikskomité, var 5 dommere samlet.

Hver af dem skal stemme for forskellige beslutninger. Afgørelsen vedtages med et flertal af stemmerne, men kun under den yderligere betingelse, at udvalgets formand stemmer for den.

Dommerne stemmer ved at trykke på knappen, der lukker kontakten under bordet, hvor de sidder. Lukker afbryderen stemmer de for og afbryder ulemperne. Tegn et simpelt diagram, der giver dig mulighed for automatisk at se afstemningsresultaterne. I det enkleste tilfælde simpelthen ved hjælp af en lyspære - oplyst - blev beslutningen taget, ikke oplyst - nej.

Opgave nummer 3. I praksis er dette usandsynligt, men som en kompleks uddannelsesopgave er det ganske passende.

I et stort sekskantet rum er der installeret en afbryder på hver væg. Byg et kredsløb, så du til enhver tid kan tænde eller slukke for lyset i rummet ved at dreje en (hvilken som helst) kontakt.

Når du uden succes har siddet over opgaver i tre til fire dage, skal du sætte dem midlertidigt til side. Og bliv travlt Boolsk algebra. Det er boolsk algebra eller, som det også kaldes, Boolsk algebra, relækredsalgebra, vil hjælpe dig med at løse dine problemer.

Hvad er boolsk algebra?

Mærkeligt nok, på trods af det faktum, at de i fem år har studeret algebra i skolen, vil mange studerende og senere voksne ikke være i stand til at besvare spørgsmålet, hvad er algebra? Algebra er en videnskab, der studerer sæt af nogle elementer og handlingerne på dem.

På et skolekursus i algebra er sådanne elementer tal. Tal kan ikke betegnes med tal, men med bogstaver, alle er bekendt med dette. I de første algebraundervisning gør det det altid svært for mange studerende. Husk, hvor vanskeligt det først var at vænne sig til at tilføje bogstaver i stedet for tal og løse ligninger, der ikke siger noget.

Sandsynligvis stillede hver af os os derefter spørgsmålet: "Hvorfor skal vi indtaste bogstaver i stedet for tal, og er det overhovedet nødvendigt?" Og først senere så du, hvilke fordele algebra giver, når du løser problemer i sammenligning med aritmetik.

Algebra bruges i mange nøjagtige videnskaber. Dette er fysik, mekanik, sopromat, elektricitet. Ohms lov der er intet mere end en algebraisk ligning: det er nok at erstatte deres numeriske værdier i stedet for bogstaver for at finde ud af, hvilken strøm der vil strømme i belastningen, eller hvilken modstand en del af kredsløbet har.

Så du blev bekendt med algebra af tal eller med elementær algebra. Den vigtigste og næsten unikke opgave er at få et svar på spørgsmålet: ”Hvad er X lig med? Hvor meget? ”

I gymnasiet studerer de begyndelsen på vektoralgebra. Denne algebra er grundlæggende forskellig fra elementær algebra. Det har en anden karakter af det studerede sæt og andre handlingsregler. Løsning af vektorligningen får vi i svaret en vektor, der ikke er et almindeligt tal, der besvarer spørgsmålet "Hvor meget?"

Formlerne for vektoralgebra adskiller sig i mange henseender fra formlerne for elementær algebra. For eksempel er der i elementær algebra og i vektoralgebra en additionsoperation. Men det udføres på helt forskellige måder.Tilføjelsen af ​​tal er slet ikke den samme som tilføjelsen af ​​vektorer.

Der er andre algebraer: lineær algebra, algebra af strukturer, algebra af ringe, algebra af logik, eller, hvad er det samme, boolsk algebra. Du har sandsynligvis ikke hørt navnet i skoletimer. George Boole - men alle kender navnet på en af ​​hans talentfulde døtre Ethel Voinich (1864 - 1960). Hun skrev romanen "Gadfly", der taler om kampen for de italienske karbonaderes rettigheder.

George Bull blev født i England den 2. november 1815. Hele sit liv arbejdede han som lærer i matematik og fysik i skolen. Fra memo- rierne fra hans studerende vides det, hvilken stor betydning Bul knyttet til udviklingen af ​​studerendes kreative evner. Da han præsenterede nyt materiale, forsøgte han at sikre, at hans studerende selv "genopdagede" bestemte formler og love.

Fortællende om studerende om de vanskeligheder, som videnskabsmænd uundgåeligt stod overfor i søgen efter sandhed, kunne læreren gerne gentage en østlig visdom: Selv den persiske trone kan ikke give så meget glæde for en person som den mindste videnskabelige opdagelse. Buhl mistede aldrig håbet om, at hans studerende en dag ville gøre en reel opdagelse.

Buhl's videnskabelige interesser var meget bredt: han var lige så interesseret i matematik og logik - videnskaben om love og former for tænkning. I disse dage blev logik betragtet som en humanioravidenskab, og mange, der kendte George Boole, var forbløffet over, hvordan de nøjagtige kognitionsmetoder, der er forbundet med matematik og rent beskrivende metoder til logik, kunne eksistere sammen i én person.

Men videnskabsmanden ville gøre videnskaben om love og former for tænkning lige så streng som enhver af naturvidenskaberne, siger matematik og fysik. Til dette begyndte Boule at betegne ikke tal som bogstaver, som det gøres i almindelig algebra, men udsagn, og viste, at sådanne ligninger, der meget ligner algebraiske, kan løse spørgsmål om sandheden og forfalskningen af ​​udsagn fra mennesket. Så den boolske algebra opstod.

Men længe før George Buhl udtrykte den tyske matematiker og filosof Gottfried Leibniz (1646-1716) først tanken om at skabe en videnskab, der ville udpege alle begreberne i almindelig tale med symboler og etablere en ny algebra til at kombinere disse symboler.

Efter oprettelsen af ​​en sådan videnskab vil forskere og filosoffer ifølge Leibniz holde op med at krangle og råbe mod hinanden, finde ud af sandheden, men de vil samle en blyant og roligt sige: "Lad os beregne!"

I dag er logikens algebra blevet en vigtig del af matematikken. En af dens opgaver er at løse alle slags ligninger, hvis numeriske forhold erstattes af alfabetiske. Hver af jer huskede sandsynligvis hele dit liv, hvordan man kunne løse ligninger af anden og tredje grad med bogstavkoefficienter. Så Boole i sin nye algebra brugte alle disse formler og regler.

Det nye i den boolske algebra er, at elementerne i det sæt, der studeres i det, ikke er tal, men udsagn. Hvis der ved løsning af almindelige algebraiske ligninger bestemmes, hvilket antal er lig med ukendt X, søger skolealgebra svaret på spørgsmålet: "Hvor meget?"

Logikens algebra er på udkig efter svaret på spørgsmålet: "Er denne eller den påstand betegnet med bogstavet X sandt?"

Betydningen og indholdet af udsagnet spiller ingen rolle her. Hver erklæring kan kun være sand eller falsk. Det kan ikke være halvt sandt og halvt falsk. Som et eksempel kan vi huske at kaste partier med en mønt.

Der betragtes kun to mønttilstande - hoveder eller haler. Efter aftale mellem parterne er ørnen JA, og halerne er NEJ. Der tages ikke hensyn til andre mellemliggende punkter i sandsynlighedsteori, selvom de er mulige. En flippet mønt kan falde på en kant, rulle ned på gulvet til benene på en stol eller et bord og forblive i en lodret position eller endda falde i et bredt hul i gulvet. (Analogt med elektriske kredsløb kan de to sidste situationer betragtes som en funktionsfejl i form af en brændt kontakt).Men i disse dage blev den boolske algebra desværre ikke udbredt.

Claude Shannon "opdagede" Buhl-algebra igen. I 1938, mens han stadig var studerende ved Massachusetts Institute of Technology and America, beviste den unge Claude, at den boolske algebra er fuldstændig velegnet til analyse og syntese af relæ- og skiftekredsløb.

Ved hjælp af boolsk algebra er det meget let at fremstille et elektrisk kredsløb til en automat, der fungerer på et relæ.For dette viser det sig, at du kun behøver at vide nøjagtigt, hvad maskinen skal gøre, det vil sige, du har brug for en algoritme til dens funktion. Så grundlaget blev lagt for teorien om digitale maskiner, der fungerer efter princippet om JA eller NEJ.

Sådan er kort fortalt historien om boolsk algebra. I de følgende artikler vil vi overveje dets grundlæggende love, eksempler på kontaktkredsløb, der implementerer disse love. Overvej løsningen af ​​de opgaver, der blev givet i begyndelsen af ​​artiklen.

Fortsættelse af artiklen: Boolsk algebra. Del 2. Grundlæggende love og funktioner

Boris Aladyshkin