Boolsk algebra. Del 2. Grundlæggende love og funktioner

Fortsættelse af historien om boolsk algebra, konventioner, regler, operationer. Overgang til det grundlæggende i kontakt kredsløb.

den første artikel George Bull blev beskrevet som skaberen af ​​logikens algebra. Den anden artikel beskriver de grundlæggende operationer i boolsk algebra og metoder til at forenkle boolske udtryk. Så Boolesk algebra bruger udsagn som argumenter og ikke deres betydning, men sandheden eller forfalskningen af ​​udsagnet.

Formularen til at skrive udtryk i boolsk algebra.

Hvis udsagnet er sandt, skrives det sådan: A = 1, hvis det er falsk, så er A = 0 (det er trods alt ikke sandt, at kartoffel er en frugt). For enhver udsagn er A enten sandt (A = 1) eller falsk (A = 0). Der kan ikke være nogen midt her. Vi har allerede talt om dette.

Hvis du forbinder to enkle udsagn med fagforeningen Og får du en kompleks erklæring, der kaldes et logisk produkt. Lad os tage to enkle ordsprog: ”Tre er mere end to” vil vi udpege med bogstav A, “Tre mindre end fem” - ved bogstav B.

Derfor er det komplekse ordsprog “Tre er mere end to Og mindre end fem” logisk (i dette tilfælde angiver store bogstaver I, at dette er en “OG” logisk operation såvel som senere i teksten “ELLER” og “IKKE.”) og B. Det betegnes som følger: A ^ B eller A * B.

Logisk multiplikation (operation "OG").

I elementær algebra A * A = A2. Men i Buhl's algebra A * A = A2 = A, A * A = A, da multiplikationstegnet (*) nu betyder ... Og ... i betydningen And ... Og. Al vores erfaring bekræfter, at A&A er den samme som A. alene. Man kan ikke være uenig i dette. Udsagnets sandhed ændres ikke, hvis den gentages af faktoren flere gange.

Produktet af to udsagn betragtes som sandt (lig med 1), da, og kun hvis begge faktorer er rigtige og falske (lig med 0), hvis mindst en af ​​faktorerne er forkert. Enig i, at disse regler ikke er i modstrid med sund fornuft, og at de desuden fuldt ud overholder reglerne for elementær algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Den første ligestilling lyder som følger: Hvis både A og B er rigtige, er produktet A * B sandt. I Buhl-algebra erstatter multiplikationstegnet (*) unionen I.

Logiske produkter inkluderer muligvis ikke to, men et større antal udsagn - faktorer. Og i dette tilfælde er produktet kun sandt, når alle udsagnsfaktorer på samme tid er sande.

Logisk tilføjelse (ELLER operation)

Hvis to udsagn er forbundet af en fagforening OR. den dannede sammensatte sætning kaldes en logisk sum.

Overvej et eksempel på en logisk sum. At sige A: "I dag går jeg på biografen."

Erklæring B: "I dag skal jeg på diskoteket." Vi tilføjer begge udsagn og får: "I dag vil jeg gå i biografen ELLER til et diskotek."

Denne komplekse erklæring betegnes som følger: A + B = C eller (A VB) = C.

Ved C betegner vi en kompleks erklæring af en logisk sum.

I det betragtede eksempel kan unionen OR ikke anvendes i en eksklusiv forstand. Faktisk kan du på samme dag komme til biografen og til diskoteket. Og her er det ordsprog:

”Formanden for havearbejde-partnerskabet vil være Petrov eller Ivanov,” er ikke en logisk sum, fordi kun én person vil være formand, og den anden vil være en almindelig amatørgartner.

V-tegnet for den logiske sum vælges, fordi det er det første bogstav i det latinske ord "vel", der betyder "eller", i modsætning til det latinske ord "aut>, der betyder" og ". Nu skal det være klart for alle, hvorfor det logiske produkt er angivet med tegnet ^.

I elementær algebra er der en regel A + A = 2A. Denne regel er sandt, uanset hvilket tal der er repræsenteret med bogstavet A. I boolsk algebra svarer reglen A + A = A til den. Vores hele livserfaring siger, at at sige A eller A eller begge A er bare en anden og længere måde at sige bare A.

Som enhver sammensat sætning kan summen af ​​de to udsagn A og B være sand eller forkert. Summen betragtes som sand, dvs. lig med enhed, hvis mindst et af udtrykkene er sandt:

A + B = 1, hvis OR A = 1 ELLER B = 1, hvilket er i overensstemmelse med konventionel aritmetik:

1+0 = 0+1 = 1.

Hvis begge summerede udsagn er rigtige, betragtes summen også som sand, derfor har vi i den boolske algebra: (1) + (1) = 1.

Beslagene er indstillet her for at understrege den betingede, betydningen af ​​denne tilføjelse og ikke aritmetik.

Summen af ​​to udsagn betragtes som falske og lig med nul, men kun hvis begge udtryk er forkert. Herfra:

0 + 0=0.

Så summen af ​​de to udsagn A + B betragtes som sand, hvis sand, ELLER A, ELLER B, ELLER begge udtryk sammen. Ordet OR betegnes således med +.

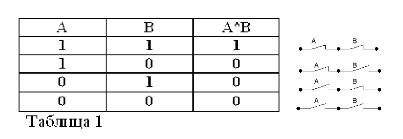
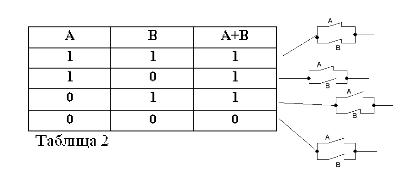
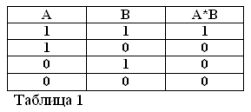
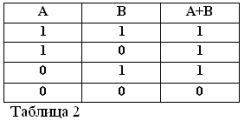
Husk, at udsagn A og B kun kan være sandt eller falsk, og derfor har et mål for sandhed 1 eller 0, kan resultaterne af de betragtede AND- og OR-operationer sammenfattes i tabel 1 og 2.

Den tredje operation, der i vid udstrækning bruges af Buhl algebra, er negationsoperationen - IKKE. Vi minder dig om, at elementær algebra bruger operationerne ADD, D Subtraher, Multiply by, Divide by og nogle andre.

For hver udsagn A er der dens negation IKKE A, som vi vil betegne med symbolet / A. Dette skulle ikke være i tvivl.

Vi giver eksempler: ”Vi vil gå i skoven” A, ”Vi vil ikke gå i skoven” / A.

Hvis udsagnet A er sandt, det vil sige A = 1, skal dets negation / A være falsk / A = 0. Og omvendt, hvis nogen erklæring er falsk, er dens negation sand. For eksempel: “En hest spiser ikke hø” / A = 0, “En hest spiser ikke hø” (A = 1). Dette kan udtrykkes i tabel 3.

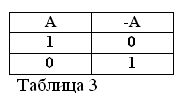
At bestemme betydningen af ​​handlingen med negation og antage, at af de to udsagn A og / A altid er en sand, følger to nye formler af boolsk algebra:

A + (/ A) = 1 og A * (/ A) = 0.

Der er også andre formler, der forenkler den logiske behandling af udsagn. For eksempel er 1 + A = 1, da summen ifølge definitionen af ​​tilføjelse, når et udtryk er lig med enhed, altid er summen lig med enhed. Det opnåede resultat afhænger ikke af, om A = 0 eller A = 1.

Hver af de tre logiske operationer, vi undersøgte (OG, ELLER, IKKE) har visse egenskaber, der er tæt på reglerne for elementær algebra. Hvis alle dem er formuleret, får vi 25 regler for boolsk algebra. De er helt nok til at løse næsten ethvert logisk problem. Uden disse regler bliver det ret vanskeligt at løse logiske problemer på grund af deres tilsyneladende kompleksitet. At forsøge at finde det rigtige svar uden at bruge reglerne betyder at erstatte dem med opfindsomhed og generelle resonnementer. Regler letter dette arbejde i høj grad og sparer tid.

Inden for rammerne af artiklen er det umuligt at overveje alle disse 25 regler, men de, der ønsker, kan altid finde dem i den relevante litteratur.

Som allerede nævnt i den første artikel i 1938 bruger den unge amerikanske videnskabsmand Claude Shannon i sin artikel ”Symbolisk analyse af relæ- og skiftekredsløb” for første gang Boolsk algebra til problemer med relæteknologi. Shannons opdagelse var, at han indså, at metoden til at designe relæmaskiner og elektroniske computere faktisk er en gren af ​​matematisk logik.

Det sker ofte. I mange år har forskeren arbejdet med et problem, der synes helt unødvendigt for hans landsmænd - bare sjovt. Men årtier og undertiden århundreder går, og en teori, som ingen har brug for, erhverver ikke kun retten til at eksistere, men uden det bliver yderligere fremskridt tænkeligt.

Hvad hjalp Shannon anden gang med at ”opdage” boolsk algebra? Sagen? Intet af den slags.

Kærligheden til relæmaskiner, bygget på konventionelle afbrydere og relæer, hjalp den unge videnskabsmand til at forbinde en glemt teori med opgaverne ved automatiske telefonudvekslinger, som han arbejdede på det tidspunkt. Senere introducerede Shannon den samme idé om "ja eller nej" i diskrete meddelelser og lagde grundlaget for en hel del af cybernetik - informationsteori.

Buhls algebra var meget velegnet til analyse og syntese af relækredsløb. Det var nok til at acceptere som et sandt udsagn: ”Der er et signal i kredsløbet”, og som et falskt - ”Der er intet signal i kredsløbet”, som en ny algebra dukkede op - signalalgebraen, relækredsløbets algebra.

Den nye algebra er kun gyldig til overvejelse af relæ- og skiftekredsløb. Når alt kommer til alt er det kun i sådanne skemaer, at betingelsen "der er et signal" og "intet signal" er opfyldt. Når signalet skifter kontinuerligt og erhverver et vilkårligt stort antal mellembetingelser (et sådant signal kaldes analog), er relæalgebra ikke relevant. Dette skal altid huskes. Men bare størstedelen af ​​elektroniske computere og cybernetiske maskiner bruger det diskrete princip om signalbehandling, der er baseret på elementerne “ja - nej”.

Udtrykket "Kontakt lukket" blev accepteret af Shannon som sandt (1) og "Kontakt åben" som falsk (0). Resten af ​​"algebra", inklusive operationerne AND, OR og NOT og 25 regler, lånte Shannon fra Boole.

Relæ-kredsløb algebra viste sig at være enklere end den boolske algebra, da den kun omhandler elementer af ja-ne-typen. Derudover er den nye algebra mere visuel.

Elementerne i denne algebra er kontakterne, som vi vil betegne med bogstaverne A, B, C ... Kontakten er lukket - A, kontakten er åben - / A (bogstav med en bindestreg).

Notationen er, som du ser, helt taget fra den boolske algebra. En åben kontakt er en negation af en lukket kontakt. Den samme kontakt kan ikke være lukket og åben.

Vi er enige om, at hvis to kontakter er betegnet med samme bogstav i et kredsløb, betyder det, at de altid har de samme værdier.

På ethvert givet tidspunkt er de enten åbne på samme tid, eller begge er lukkede. Den nemmeste måde at forestille sig dem mekanisk forbundet sammen, så begge af dem åbner eller lukker samtidig.

Hvis en kontakt i en eller anden kæde er en negation af en anden kontakt, er deres betydning altid modsat. For eksempel kan kontakter C og / C aldrig være åbne eller lukket samtidigt. Og i diagrammet kan de repræsenteres mekanisk forbundet: Hvis en af ​​dem åbner, lukker den anden.

Vi begynder vores bekendtskab med relæalgebra ved at analysere de enkleste kredsløb svarende til funktionerne AND, OR og NOT.

Produktet fra to kontakter (betjening OG) er det kredsløb, der opnås som et resultat af deres serieforbindelse: det er kun lukket (lig med 1), når begge kontakter er lukket (lig med 1).

Summen af ​​to kontakter (ELLER drift) vil være kredsløbet, der dannes, når de er parallelt forbundet: det er lukket (lig med 1), når mindst en af ​​kontakterne, der danner kredsløbet, er lukket (lig med 1).

Det modsatte af denne kontakt (operation IKKE) er en kontakt, der er lig med 0 (åben), hvis denne kontakt er 1 (lukket), og vice versa.

Som i den boolske algebra, hvis kontakterne er betegnet med bogstaverne A og B, vil vi betegne produktet af to kontakter med A * B, summen med A + B og kontakten overfor A, med / A. Ovenstående er forklaret i figur 1, 2 og 3.

Gyldighed af tabeller svarende til funktionerne AND, OR og NOT. nu skal ingen være i tvivl.

Lad os dvæle ved to eksempler: 1 * 0 = 0 og 1 + 0 = 1.

Det ses af figuren, at en permanent lukket kontakt, der er forbundet i serie med en konstant åben kontakt, svarer til en permanent åben kontakt (1 * 0 = 0) En permanent lukket kontakt, der er forbundet parallelt med en konstant åben kontakt, svarer til en permanent lukket kontakt.

Når du er blevet bekendt med aritmetikken i kontaktkredsløb, kan du beskrive ethvert relækredsløb med en formel ved hjælp af de accepterede konventioner. I cybernetik kaldes sådanne formler strukturelle.

Hvis strukturformlen for et hvilket som helst relækredsløb er 1, kan et signal passere gennem det - kredsløbet er lukket. Omvendt, hvis strukturets formel for kredsløbet er 0, passerer signalet ikke gennem det - kredsløbet er ødelagt.Konklusion: to relækredsløb er ækvivalente med hinanden, når deres strukturformler er ens.

I fortsættelsen af ​​artiklen vil vi overveje eksempler på kontaktkredsløb, typiske kontaktkredsløb og deres ækvivalenter samt udarbejde diagrammer i henhold til strukturformler. Vi overvejer også de vigtigste logiske kredsløb, der udfører funktionerne i den boolske algebra.

Fortsættelse af artiklen: Boolsk algebra. Del 3. Kontaktordninger

Boris Aladyshkin

Comments

[#1 Alex]

Tak

Kun et punkt, afsnit:

"Som i den boolske algebra, hvis kontakterne er betegnet med bogstaverne A og B, vil vi betegne produktet af to kontakter med A * B, summen med A + B og kontakten overfor A, med / A. Ovenstående er forklaret i figur 1, 2 og 3 ..."

Hvor er figur 3?