kategorier: Udvalgte artikler » Begynderelektrikere
Antal visninger: 57937
Kommentarer til artiklen: 4
Boolsk algebra. Del 3. Kontaktordninger
 Artiklen beskriver de grundlæggende principper for design af relækredsløb i overensstemmelse med en given algoritme for deres funktion.
Artiklen beskriver de grundlæggende principper for design af relækredsløb i overensstemmelse med en given algoritme for deres funktion.
I to tidligere artikler fik at vide om det grundlæggende Boolsk algebra og relæalgebra. På dette grundlag blev strukturelle formler udviklet, og allerede typiske kontaktkredsløb blev udviklet på dem.
Det er en simpel sag at udarbejde en strukturformel i henhold til et færdigt skema. Det er meget vanskeligere at præsentere det fremtidige maskins elektriske kredsløb i henhold til den færdige konstruktionsformel. Det har brug for lidt træning!
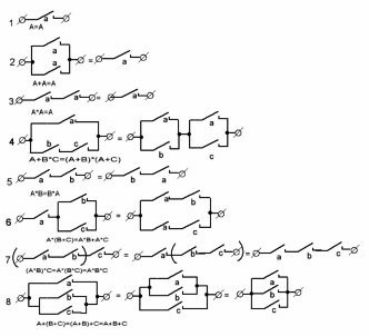
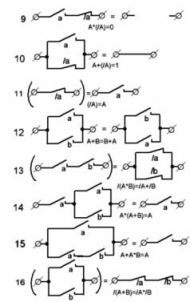
Figur 1 viser de mest almindelige indstillinger. kontakt kredsløb og deres ækvivalenter. De vil hjælpe med at forberede elektriske kredsløb til maskiner samt analysere færdige strukturer, for eksempel i processen med at reparere dem.
Hvordan kan du bruge mulighederne for kontaktkredsløb diskuteret ovenfor?
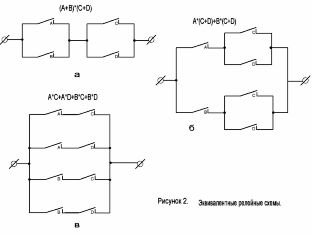
Overvej kredsløbet vist i figur 2, a. Den tilsvarende strukturformel har formen: (A + B) * (C + D).
Ved hjælp af distributionsloven for den boolske algebra åbner vi parenteserne i dette udtryk og får: A * (C + D) + B * (C + D), som svarer til skemaet vist i figur 2, b. På grund af multiplikation kan vi endvidere opnå formlen A * C + A * D + B * C + B * D, svarende til figur 2, c.
Alle tre ordninger er ækvivalente, det vil sige, de viser sig at være lukkede under de samme betingelser. De er dog forskellige i kompleksitet.
Figur 1. Typiske kontakt kredsløb
Den første af kredsløbene, den enkleste, den kræver fire relæer, som hver skal have en normalt åben kontakt. (For at forenkle tegningerne vises ikke relæspoler).
Skema "b" kræver et relæ med to kontaktgrupper. Faktisk er den vigtigste opgave for algebraen for kontaktkredsløb at finde alle ækvivalente kredsløb, så du kan vælge den enkleste blandt dem.
Figur 2. Ækvivalente kontakt kredsløb.
For at konsolidere det dækkede materiale, prøv selv at løse følgende problemer.
1. Tegn kredsløbsdiagrammet for en automat med strukturformlen A * B * C * D + A * B * E + A * D.
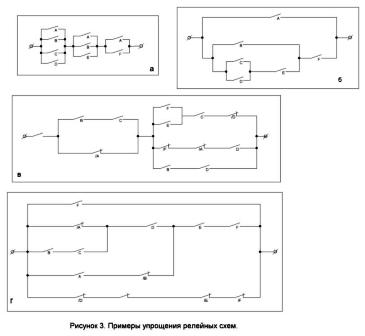
2. Bevis at kredsløbene vist i figur 3, a og b, er ækvivalente.
3. Forenkle kredsløbet vist i figur 3, c.
4. Hvilken strukturformel implementerer skemaet i figur 3, d?
Efter det, vi allerede har undersøgt, vil det være muligt at begynde at løse de problemer, der blev sat lige i begyndelsen af den første artikel. Vi husker dem kort.
Den første opgave var at tænde og slukke for pæren i rummet med tre afbrydere placeret forskellige steder: ved døren, ved bordet, ved sengen.
Den anden opgave er at stemme sportsdommere: ud af fire dommere skal ”FOR” stemme mindst to, forudsat at ”FOR” kommissionsformand stemte.
Den tredje opgave var kun til uddannelsesmæssige formål. Det foreslog det samme som i det første, kun for seks afbrydere, som om der var seks vægge i rummet. Lignende kredsløb er lige ved at blive udviklet ved hjælp af algebra fra relækredsløb.
Generelt, hvis vi ønsker at udvikle et skema, der har nogle givne logiske egenskaber, kan vi nærme os dette problem på to forskellige måder. Konventionelt kan disse stier kaldes "intuitiv" og "algebraisk".
Nogle opgaver løses bedre på den første måde, mens andre på den anden. Den intuitive tilgang viser sig at være mere praktisk, når betjeningen af kredsløbet styres af mange afbrydere, men der er en vis symmetri i det gensidige arrangement af disse relæer. Vi vil se, at her en intuitiv tilgang fører hurtigere til målet, mens brugen af relæalgebraapparatet i tilfælde af mange variabler kan være meget besværligt. Det er nyttigt at blive bekendt med begge mulige tilgange til løsning af dette problem.
Lad os starte med en intuitiv tilgang. Antag, at vi havde brug for at opbygge et kredsløb, der var lukket, når alle n kontrolrelæ kredsløb fungerede.
Løsningen på dette problem kræver ikke lang overvejelse: det er tydeligt, at den indstillede betingelse er opfyldt, hvis der sammenkobles sekventielt n normalt åbner relækontakter.
Tilsvarende er det indlysende, at det for at opbygge et kredsløb, der lukker, når mindst et af n-relæerne er udløst, er det nok at forbinde n normalt åbne relækontakter parallelt.
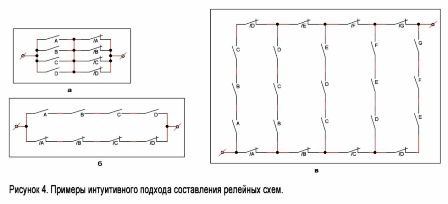
Det er let at forestille sig et kredsløb, der lukker, når nogle, men ikke alle, relæer udløses. Et sådant kredsløb er vist i figur 4, a. Til højre er et diagram, der fungerer på princippet om "alt eller intet." Det lukkes kun, når alle relæer er aktiveret, eller relæerne er afbrudt (figur 4, 6).
Overvej nu et mere komplekst eksempel. Antag, at der er n kontakter, der er placeret i en bestemt specifik sekvens: A, B, C, D, E, F ... Vi konstruerer et kredsløb, der lukker, når eventuelle k-seriekoblede kontakter er lukket, og kun de er. Et sådant skema for værdierne n = 7 og k = 3 er vist i figur 4, c. Fremgangsmåden til konstruktion af sådanne skemaer til andre værdier for n og k er tydelig fra dette figur.
Vi fortsætter med at konstruere kredsløb i henhold til de givne betingelser for deres arbejde ved hjælp af relæalgebra.
Som før er driftsbetingelserne for kredsløbet altid altid først indstillet mundtligt. Designeren skal først og fremmest kunne sætte ord på, hvad han vil. Hvis han ikke har sådan klarhed, hjælper ingen algebra. Du skal altid starte med en klar redegørelse for de krav, der er stillet inden den nye ordning. Som i enhver virksomhed er denne opgave måske den sværeste. Hvis betingelserne er enkle nok, kan vi straks skrive et udtryk for en strukturformel, der opfylder disse krav.
Eksempel 1 Antag, at vi er nødt til at opbygge et kredsløb, der indeholder 4 ben A, B, C og D, så kredsløbet tændes, når kontakt A er lukket, og en af de andre tre kontakter. I dette enkle tilfælde vil betjeningen af kredsløbet i verbal notation se sådan ud: “Kredsløbet skal lede strøm, hvis kontakter A og B er lukket, eller kontakter A og C eller kontakter A og D. Enig i, at det nu er meget simpelt at udarbejde en strukturformel. Det ser sådan ud:
A * B + A * C + A * D = 1 eller A * (B + C + D) = 1.
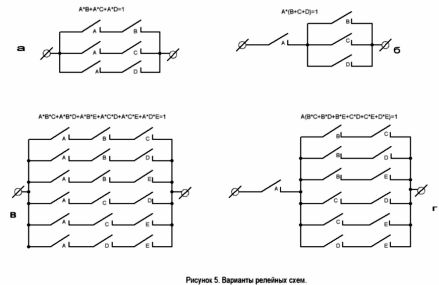
Kredsløbet har to muligheder. De er vist i figur 5. Den anden mulighed kræver ikke et relæ med tre normalt åbne kontakter.
Eksempel 2 Den første artikel var opgave nummer 2 om afstemning af sportsdommere. Læs dens tilstand nærmere, det ligner det eksempel, der netop er undersøgt. En tydeligere verbal registrering af kravene vil se sådan ud: ”Det er nødvendigt at tegne et kredsløb, der indeholder 5 kontakter A, B, C, D, E, så det leder strøm og tænder displaylampen, hvis følgende kontakter er lukket:
A og B og C eller A og B og D eller A og B og E eller A og C og D eller A og C og E eller A og D og E. Kontakt A er formandsknappen. Hvis det ikke presses, vil hver af de 6 logiske produkter være 0, dvs. Afstemningen fandt ikke sted.
Strukturformlen er som følger:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
eller A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Begge varianter af kredsløbet er vist i figur 5, c og d. Dette er løsningen på problemet.
Når du har en vis færdighed i at læse strukturformler, er det let at forestille sig kredsløbet til selve automaten og alle dens muligheder. Interessant nok giver algebraen i relækredsløb mere information end endda selve kredsløbet. Det giver dig mulighed for at se, hvor mange og hvilke relæer der kræves. Med sin hjælp kan du nemt finde den enkleste version af kredsløbsmaskinen.
Eksempel 3 Efter at have fået nogle erfaringer med udarbejdelsen af strukturformler, vil vi forsøge at løse det problem, der startede første artikel: du er nødt til at designe en afbryder, der giver dig mulighed for at tænde lyset, når du går ind i indgangen og slukke for det, efter at du er klatret til det ønskede gulv, eller omvendt, tænd det, når du forlader lejligheden og slukke for det, efter at du er gået ned. Den samme situation sker i en lang korridor: i den ene ende skal pæren være tændt, og efter at have gået til den anden ende slukket. Kort sagt, opgaven koges ned til at styre en pære fra forskellige steder med to kontakter.
Vi vælger følgende procedure til løsning af problemet: først formulerer vi tydeligt driftsbetingelserne for switchene, så skriver vi dem i form af en formel, og vi tegner et elektrisk kredsløb baseret på dem.
Så at pæren brændte (1), er det nødvendigt, at en af to betingelser var opfyldt:
1. Tænd for kontakten i bunden (A), og sluk øverst (/ B). Gå ind i verandaen.
2. Tænd for kontakten øverst (B), og sluk for bunden (/ A). Forlad lejligheden.
Ved hjælp af den accepterede notation skrives strukturformlen som følger:
A * (/ B) + (/ A) * B = 1
Kredsdiagrammet for afbryderen er vist i figur 6. I øjeblikket er sådanne afbrydere kommercielt tilgængelige, disse er de såkaldte gennemgangskontakter. Derfor er overvejelserne om disse ordninger her kun givet til begrebet de generelle principper for deres arbejde.
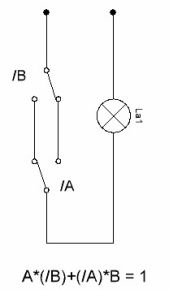
Figur 6
I opgave nr. 1 i begyndelsen af den første artikel, talte vi om et skema, der giver dig mulighed for at tænde og slukke for lyset i rummet med en af de tre afbrydere. Ræsonnerer på samme måde som i tilfælde af to kontakter, får vi strukturformlen:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
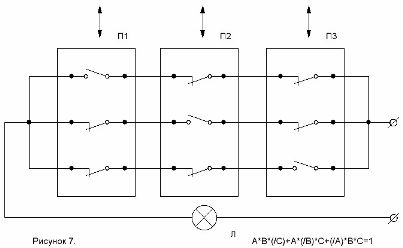
Skemaet udarbejdet med denne formel er vist i figur 7.
Figur 7
I begyndelsen af den første artikel blev en enkel uddannelsesopgave nr. 2 foreslået: som om der var seks vægge i rummet, og hver af dem havde en switch. Kredsløbets logik er nøjagtigt den samme som for de tre kontakter. Lad os betegne dem med bogstaverne A, B, C, D, E, F. Husk, at notationen (/ A), (/ B) og så videre, dette ikke er et delingstegn, men en logisk negation. Oftere angivet med understregning af karakterer og endda hele udtryk øverst. I nogle skemaer erstattes denne understregning simpelthen med et minustegn. Så strukturformlen for de seks switches er:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Læserne opfordres til at udarbejde et komplet elektrisk kredsløb, der implementerer denne strukturformel for at tilegne sig praktiske færdigheder i design af kredsløb. Et lille tip: til kredsløbet har du brug for seks relæer, der hver har en normalt åben kontakt og fem normalt lukket. Sådanne komplekse relæer kan om nødvendigt samles fra flere enklere ved at forbinde deres spoler parallelt.
Dermed afsluttes historien om boolsk algebra og algebraen for relækredsløb.
Fortsættelse af artiklen: Logiske chips
Boris Aladyshkin
Se også på elektrohomepro.com
: